- #1
Soren4
- 128
- 2
I studied Taylor series but I would like to have an answer to a doubt that I have. Suppose I have ##f(x)=e^{-x}##. Sometimes I've heard things like: "the exponential curve can be locally approximated by a line, furthermore in this particular region it is not very sharp so the approximation is even more good.."
Now I'm aware of the fact that any function (differentiable and so on) can be approximated by a line and further polynomial, but consider this graph of ##f(x)## and the regions ##A## and ##B##.
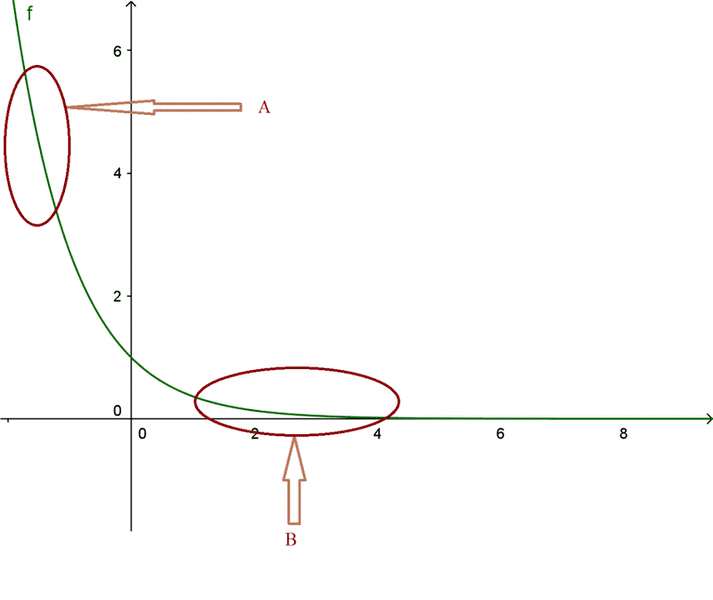
My question is : to what extent I can say "##f(x)## is better approximated by a line in ##B## than in ##A##"? And, if I could do this, why is that ? Is that because in region ##B## ##f(x)## is less sharp than in ##A##, or is there other reason behind this?
Now I'm aware of the fact that any function (differentiable and so on) can be approximated by a line and further polynomial, but consider this graph of ##f(x)## and the regions ##A## and ##B##.
My question is : to what extent I can say "##f(x)## is better approximated by a line in ##B## than in ##A##"? And, if I could do this, why is that ? Is that because in region ##B## ##f(x)## is less sharp than in ##A##, or is there other reason behind this?