I Is Callen right in claiming dQ=TdS for all quasi-static processes?

[Anna57]

TL;DR Summary

A question regarding the validity of the relationship $$dQ=TdS$$ for all quasi-static processes. Based on Callen's Thermodynamics.

Hello!

I am currently reading the second edition of Callen's Thermodynamics and an Introduction to Thermostatistics, and I have a question regarding Callen's definition of quasi-static. On page 96, Callen says:

Consider an arbitrary curve drawn on the hypersurface of Fig. 4.3*, from an inital state to a terminal state. Such a curve is known as a quasi-static process. A quasi-static process is thus defined in terms of a dense succession of equilibrium states.

*Fig. 4.3, the hypersurface defined by the entropy function graphed in its configuration space

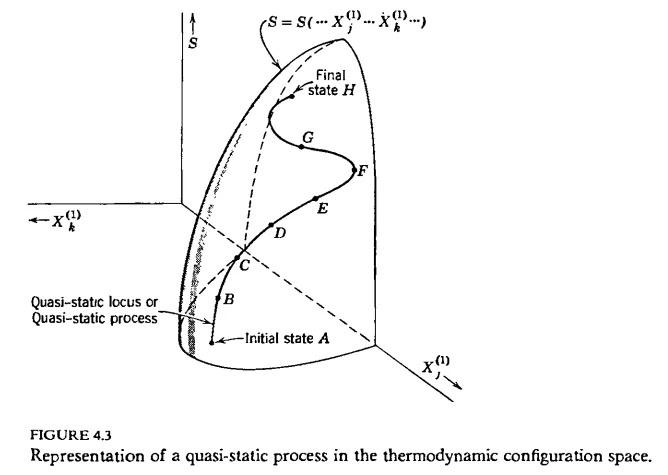
Another way of characterizing Callen's definition is that a process is quasi-static if it traces out a continuous curve in the system's configuration space. So far it's all well and good. A little later, Callen claims that the identification of $$TdS$$ as the heat transfer is only valid for a quasi-static process. In seemingly the rest of the book, he takes this to be a necessary criterion for quasi-staticity. A process which does not obey $$dQ=TdS$$, no matter how well it seems to fit the original definition in terms of equilibrium states, is apparently not quasi-static. I am having a lot of trouble understanding how Callen draws this conclusion as it is not motivated and other motivations later on are predicated on this being true. Is it possible to prove, based on the definition of quasi-staticity given above, that it necessarily follows that $$dQ=TdS$$ for any, arbitrary quasi-static process? I have searched far and wide but cannot find any general proof. I am having trouble believing it is even true, and sources online even seem to disagree.

 

[Lord Jestocost]

The following publication might be of help for you:

‘The impossible process: thermodynamic reversibility’ by John D. Norton (Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 55, pp. 43–61)

Abstract
Standard descriptions of thermodynamically reversible processes attribute contradictory properties to them: they are in equilibrium yet still change their state. Or they are comprised of non-equilibrium states that are so close to equilibrium that the difference does not matter. One cannot have states that both change and no not change at the same time. In place of this internally contradictory characterization, the term “thermodynamically reversible process” is here construed as a label for a set of real processes of change involving only non-equilibrium states. The properties usually attributed to a thermodynamically reversible process are recovered as the limiting properties of this set. No single process, that is, no system undergoing change, equilibrium or otherwise, carries those limiting properties. The paper concludes with an historical survey of characterizations of thermodynamically reversible processes and a critical analysis of their shortcomings.