Is interchanging the order of the surface and volume integrals valid here?

[Beelzedad]

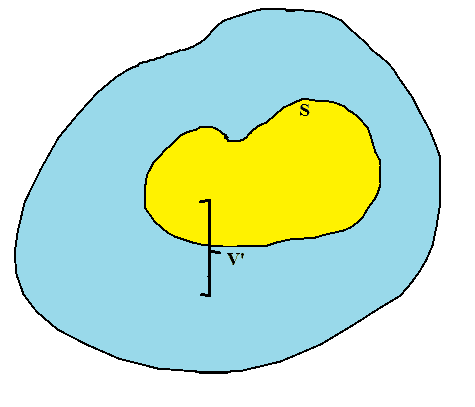
Consider a continuous charge distribution in volume $V'$. Draw a closed surface $S$ inside the volume $V'$.

Consider the following multiple integral:

$\displaystyle A=\iiint_{V'} \left[ \iint_S \dfrac{\cos(\hat{R},\hat{n})}{R^2} dS \right] \rho'\ dV' =4 \pi\ m_s$

where

$R=|\mathbf{r}-\mathbf{r'}|$

$\mathbf{r'}=(x',y',z')$ is coordinates of source points

$\mathbf{r}=(x,y,z)$ is coordinates of field points

$\cos(\hat{R},\hat{n})$ is the angle between $R$ and normal to surface element

$\rho'$ is the charge density and is continuous throughout the volume $V'$

$m_s$ is the total charge inside surface $S$
______________________________________________________________________________________

Also consider the following multiple integral:

$\displaystyle B= \iint_S \left[ \iiint_{V'} \dfrac{\cos(\hat{R},\hat{n})}{R^2} \rho'\ dV' \right] dS$

where the symbols have the meanings stated above.

\begin{align}
B &= \iint_S \left[ \iiint_{V'} \rho' \dfrac{\hat{R} \cdot \hat{n}}{R^2} \ dV' \right] dS\\
&=\iint_S \left[ \iiint_{V'} \rho' \dfrac{\hat{R} }{R^2} \ dV' \right] \cdot \hat{n}\ dS\\
&=\iint_S \mathbf{E} \cdot \hat{n}\ dS
\end{align}
_____________________________________________________________________________________

Is $A=B\ ?$

i.e. Is interchanging the order of surface and volume integration valid? I know it is usually valid but my doubt is due to the following reasons:

1. In the surface integral of equation $A$, when $\mathbf{r'} \in S$, we can only use spherical coordinate system with origin at point $\mathbf{r'}$ (in order to avoid improper integral with limits). So while computing $A$, we cannot use only one coordinate system. Instead, we have to use infinitely many coordinate systems.
2. In the volume integral of equation $B$, for all $\mathbf{r}$, i.e. for all $\mathbf{r} \in S$, we can only use spherical coordinate system with origin at point $\mathbf{r}$ (in order to avoid improper integral with limits). So while computing $B$, we cannot use only one coordinate system. Instead, we have to use infinitely many coordinate systems.

Note:

I know $\int \left[\int f(x,y)\,dx \right]dy = \int \left[\int f(x,y)\,dy \right]dx$ is true usually. Also, if in the diagram, if the volume $V'$ is contained within the surface $S$, then it is valid to change the order of integration. But here the issue is a little different. The surface $S$ is inside the volume $V'$ (please have a look at my diagram) and thus improper integral comes into play.

While computing $A$, if we need to avoid improper integrals, we have no choice except to work with infinitely many spherical coordinate systems each having their origin at points $\in V'$.

Similarly while computing $B$, if we need to avoid improper integrals, we have no choice except to work with infinitely many spherical coordinate systems each having their origin at points $\in S$.

Then how is it valid to change the order of integration in this situation? That is, how can $A=B?$

 

[mitochan]

Hi.

I have a question about the case. As for A, m_s is expressed as
$$\int_{V'} \rho' dV' = m_s$$
thus if your equation holds,
$$\int_S \frac{cos(\mathbf{R}\cdot\mathbf{n})}{R^2}dS=4\pi$$
I am afraid LHS integral is zero for the field source point outside S. Is it always enclosed by S?
Here I did not used symbols $\int\int$ and $\int\int\int$ to express surface and volume integral as you do. Instead I wrote a single integral.

 

[Beelzedad]

Hi.

I have a question about the case. As for A, m_s is expressed as
$$\int_{V'} \rho' dV' = m_s$$
thus if your equation holds,
$$\int_S \frac{cos(\mathbf{R}\cdot\mathbf{n})}{R^2}dS=4\pi$$
I am afraid LHS integral is zero for the field source point outside S. Is it always enclosed by S?
Here I did not used symbols $\int\int$ and $\int\int\int$ to express surface and volume integral as you do. Instead I wrote a single integral.

I really apologize for not being able to mention it. It seemed to me to be too obvious for you.

Let $U'$ denote the volume enclosed by surface $S$. Then:

$\displaystyle \iiint_{U'} \rho' dU' = m_s \tag1$

For field point inside $S$:

$\displaystyle \iint_S \dfrac{\cos(\hat{R},\hat{n})}{R^2} dS=4 \pi \tag2$

For field point on $S$:

$\displaystyle 0<\iint_S \dfrac{\cos(\hat{R},\hat{n})}{R^2} dS<4 \pi \tag3$

For field point outside $S$:

$\displaystyle \iint_S \dfrac{\cos(\hat{R},\hat{n})}{R^2} dS=0 \tag4$

And lastly, the volume integral over $V'$ of these (surface integrals) is given by $A$. My book has a bit lengthy derivation of it ($3$-$4$ pages). It may not be needed in answering this question. My question is only about the interchanging of order of surface and volume integrals in this situation. But if you really need the $3$-$4$ pages derivation, it will take me some time to type it down.

 

[mitochan]

Thanks for explanation. The integral

$$\int_{S}\int_{V'}[\ \rho(r')\frac{\mathbf{r}-\mathbf{r'}}{|\mathbf{r}-\mathbf{r'}|^3}\ ]\cdot d\mathbf{S}\ dV'$$
where integration parameters r is on S and r' is in V', are interpreted as for orders "first prime then no-prime"

$$\int_{S}[\ \int_{V'}[\ \rho(r')\frac{\mathbf{r}-\mathbf{r'}}{|\mathbf{r}-\mathbf{r'}|^3}\ ]dV' \ ]\cdot d\mathbf{S}$$
which means "Find electric field generated from all the charges in V' working on a point of surface S first and then integrate their projection on S" , and "first no-prime then prime"
$$\int_{V'}[\ \int_{S}[\ \rho(r')\frac{\mathbf{r}-\mathbf{r'}}{|\mathbf{r}-\mathbf{r'}|^3}\ ]\cdot d\mathbf{S}\ ] \ dV'$$
which means "Find electric field contribution of a charge projected on all over the surface S , then integrate it for all the charges in V'". The both meet.