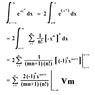KoopaCooper
- 6
- 0
OK, this is going back to a problem I studied back in Calculus class; it's been a few years since I graduated, so bear with me please... :)
It's easy to integrate \int^{\infty}_{-\infty}\\e^{-mod(x)}\\dx (giving a value of 2), and with a bit of grunt-work, the same can be done for \int^{\infty}_{-\infty}\\e^{-mod(x^2)}\\dx (giving the value of \sqrt{\pi}). But I was curious about \int\\e^{-mod(x^n)} for values of n>2.
Would it be considered valid to take the power series of the function and integrate it, then evaulate that at the end points?
For example, for the general case of x to an nth power... (oh heck...I tried to used the forum code but it got so tangled up...here's one I MSPainted earlier instead).
My question is, is this integration and evaluation valid? Have I integrated it properly? Does it count? (I never did check if the integrated power series converges). It certainly appears to work when I evaluated the partial sums of the series with x tending towards infinity, for the cases of m=1 and m=2, but is it legal?
It's easy to integrate \int^{\infty}_{-\infty}\\e^{-mod(x)}\\dx (giving a value of 2), and with a bit of grunt-work, the same can be done for \int^{\infty}_{-\infty}\\e^{-mod(x^2)}\\dx (giving the value of \sqrt{\pi}). But I was curious about \int\\e^{-mod(x^n)} for values of n>2.
Would it be considered valid to take the power series of the function and integrate it, then evaulate that at the end points?
For example, for the general case of x to an nth power... (oh heck...I tried to used the forum code but it got so tangled up...here's one I MSPainted earlier instead).
My question is, is this integration and evaluation valid? Have I integrated it properly? Does it count? (I never did check if the integrated power series converges). It certainly appears to work when I evaluated the partial sums of the series with x tending towards infinity, for the cases of m=1 and m=2, but is it legal?