ecneicScience
- 8
- 2
My question is: suppose you have a function ##F(x)## which has an asymptote at ##x=x*##. Can you decompose ##F(x)## so that
$$F(x) = G(x) + H(x)$$
where ##G(x)## is defined at ##x=x*## and ##H(x)## contains the asymptotic behaviour at ##x=x*## and goes to ##0## at plus or minus ##\inf##? This is commonly done when ##F(x)## is a polynomial in order to approximate ##F(x)##'s behaviour with the function ##G(x)## when ##x## is sufficiently far away from ##x^{*}##.
I have a very complicated function ##F(x)## that I would like to extract ##G(x)## from. If you're curious here it is:
$$F(x) = \frac{(2 a_1 z^{-a_2} -2 a_1 z^{-a_1} + z^{-a_1} - z^{-a_2}+ a_1^2 z^{-a_1} - a_2^2 z^{-a_2}) ln(z)^2 + (2 a_2 z^{-a_2} -2 a_1 z^{-a_1}+2 z^{-a_2} - 2 z^{-a_1}) ln(z) + 2 z^{-a_1} - 2 z^{-a_2}}
{(a_1 z^{-a_1} - a_2 z^{-a_2} + z^{-a_2} - z^{-a_1}) ln(z)^2 + (z^{-a_1}-z^{-a_2}) ln(z)}$$
where
$$z = 10^{x-x^{*}}$$
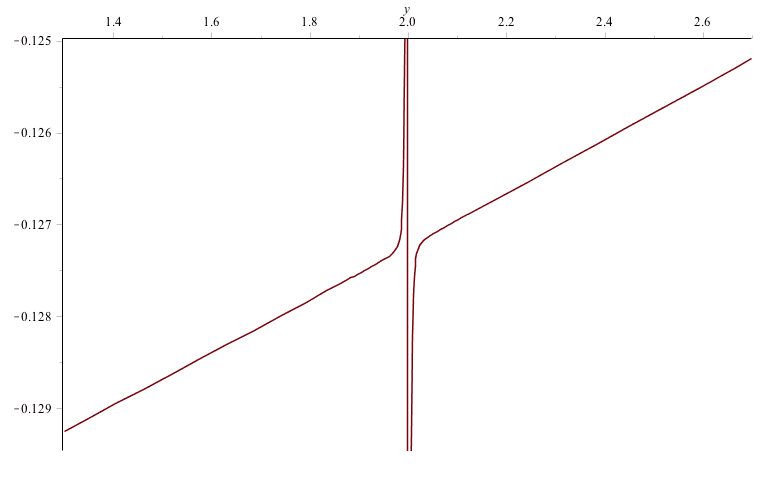
and ##a_2>a_1>0## and ##x^*>0##. I've attached a graph for an instance of the function where ##x^{*}=2##. As you can see there is an asymptote at ##x=2##. I want either ##G(x)## or the slope of ##G(x)## at ##x=x^{*}##. Has anyone encountered a similar problem?
$$F(x) = G(x) + H(x)$$
where ##G(x)## is defined at ##x=x*## and ##H(x)## contains the asymptotic behaviour at ##x=x*## and goes to ##0## at plus or minus ##\inf##? This is commonly done when ##F(x)## is a polynomial in order to approximate ##F(x)##'s behaviour with the function ##G(x)## when ##x## is sufficiently far away from ##x^{*}##.
I have a very complicated function ##F(x)## that I would like to extract ##G(x)## from. If you're curious here it is:
$$F(x) = \frac{(2 a_1 z^{-a_2} -2 a_1 z^{-a_1} + z^{-a_1} - z^{-a_2}+ a_1^2 z^{-a_1} - a_2^2 z^{-a_2}) ln(z)^2 + (2 a_2 z^{-a_2} -2 a_1 z^{-a_1}+2 z^{-a_2} - 2 z^{-a_1}) ln(z) + 2 z^{-a_1} - 2 z^{-a_2}}
{(a_1 z^{-a_1} - a_2 z^{-a_2} + z^{-a_2} - z^{-a_1}) ln(z)^2 + (z^{-a_1}-z^{-a_2}) ln(z)}$$
where
$$z = 10^{x-x^{*}}$$
and ##a_2>a_1>0## and ##x^*>0##. I've attached a graph for an instance of the function where ##x^{*}=2##. As you can see there is an asymptote at ##x=2##. I want either ##G(x)## or the slope of ##G(x)## at ##x=x^{*}##. Has anyone encountered a similar problem?
Last edited: