Is MIT Prof. Lewin wrong about Kirchhoff's law?

[yungman]

Would you like to provide an example?

Don't know, some people here said it fail in some cases, all I want to say is I do not defend KVL, I only say KVL hold in this case.

Can you tell me your opinion with my assertion that the whole thing is just FL where a magnetic pulse induce a voltage in the loop and when taking into account of the voltage source, KVL hold.

 

[Studiot]

I explicitly showed how to apply Kirchoff to the problem in hand in my post#100.

I also displayed an example of where FL is inapplicable, but Kirchoff is applicable in my post#32.

Perhaps they were so short they slipped by notice?

To find examples of inapplicability, simply look at the conditions of validity of the theorem or equation or law.

FL requires a changing magnetic field. Hence post#32.

Kirchoff requires a complete loop.

 

[stevenb]

and when taking into account of the voltage source, KVL hold.

Which definition of KVL are you claiming is upheld in Prof. Lewin's example?

The version that the Prof gave was that the sum of potentials around a loop equal zero. Do you understand that the transformer EMF you are calling the lumped or distributed voltage source is not a potential? If you understood this you would not claim his definition of KVL is upheld.

Also, the version of KVL from the other MIT lecture is not upheld in the sense that the starting assumption is not true in this example.

So, this point you are trying to make is unclear to me. Telling us your accepted definition of KVL would help clarify and give us a chance of understanding your points.

 

[yungman]

Faraday’s and Kirchoff’s laws were developed for different circumstances and are therefore different.
Both sometimes apply to situations not covered by the other; neither is a special case of the other.

I am in general agreement with Prof Lewin in his statements, with the exception that I have no trouble applying the original form of Kirchoff’s law to his apparatus.

It is instructive to consider the original form of both laws to see where they overlap and where they differ. It should be remembered that in their time magnetism was treated in terms of ‘lines of force’.

This is Maxwell’s translation of Kirchoff



They went on to state that this sum is known as the total EMF in a circuit (loop).


And this is Nightingale's record of Faraday



My understanding of Faraday's law is that it is in differential form as stated here. It is more far reaching than Kirchoff’s Law as it connects electric and magnetic effects. Kirchoff 's Law relates purely to electric effects. However the downside of this is that there must actually be magnetic flux to vary to yield the EMF.

Further differences are that Faraday does not require a closed loop, although he does not prohibit one either.
Kirchoff’s treatise concerned loops in meshes. He does not actually mention potential difference or drop and he does not distinguish between sources of EMF. They are all the same to him.

So to apply Kirchoff to Lewin proceed as follows:

The sum of the EMF's = The sum of the IR products

Used in this form it appears to me that the law is satisfied.

The total EMF in the circuit is 1 volt (the EMF induced by the coil) and the IR sum is 0.9 + 0.1 volt.

I believe it used to be phrased in this way to allow for just such a situation.

What has Lewin done then?

Well there is only one source of EMF in the loop and it is distributed around the whole loop. It is not lumped into any particular circuit element and cannot be applied at any particular point in the loop.
I think we are in agreement on this point that the mag field induce emf into the loop and is distributed around the whole loop. That was the reason I suggested to do the experiment over with resistors making up the whole loop instead of having long section of wire as part of the loop.
This brings out the difference between EMF (which is distributed around the circuit in this case) and Potential Difference or Potential Drop.
But as I said, the professor specifically said he measure the voltage across the resistors going clockwise and counter clockwise. That is potential. He claimed he can measure different voltages but he took the wire as a single point rather than part of the loop.
So Prof Lewin has demonstrated is that an EMF and a Potential Difference are not two names for the same thing. They are in fact different animals.
I don't even think this is relavent for what he tried to claim. He used the voltage drop as an argument. It is PD that he was using.
The give away clue is in his statement about conservative and non conservative fields.

For PD the line intergral $$\oint$$E.dl is zero around the loop.
For EMF it is not.

Another way to look at it is that an EMF is capable of introducing energy into the system, but PD is not.

A third way to look at it is to note that PD's result from the solution of Laplaces equation, EMF's result from the solution of Poissons equation, where there is a forcing function.

I am not disagreeing with you on the points you make, I just disagree with the experiment he used to derive his argument. And the whole point is if the experiment was done wrong, there is no point of going any further and nothing can derive out of what he said. One can not over look the flaud of the experiment and continue the argument of the theory.

 

[yungman]

I explicitly showed how to apply Kirchoff to the problem in hand in my post#100.

I also displayed an example of where FL is inapplicable, but Kirchoff is applicable in my post#32.
Of cause FL is not applicable, there is no external magnetic field. I don't even see your point.
Perhaps they were so short they slipped by notice?

To find examples of inapplicability, simply look at the conditions of validity of the theorem or equation or law.

FL requires a changing magnetic field. Hence post#32.

Kirchoff requires a complete loop.

........

 

[yungman]

Which definition of KVL are you claiming is upheld in Prof. Lewin's example?

The version that the Prof gave was that the sum of potentials around a loop equal zero. Do you understand that the transformer EMF you are calling the lumped or distributed voltage source is not a potential? If you understood this you would not claim his definition of KVL is upheld.
It is my understanding that when you start measuring the voltage drop around the loop, it is potential. AND if he stop treating the connecting wire as a point or a note only, then he should measure the VOLTAGE drop along the wire also, then the sum of all VOLTAGE around the loop is zero and KVL hold. Once the EMF is induced into the loop, it become REAL VOLTAGE and should be treated accordingly.
Also, the version of KVL from the other MIT lecture is not upheld in the sense that the starting assumption is not true in this example.

So, this point you are trying to make is unclear to me. Telling us your accepted definition of KVL would help clarify and give us a chance of understanding your points.

My understanding of KVL is you include all the voltage drop across the components and the VOLTAGE is zero around a closed loop. I tread induced EMF as voltage source. How can you not treating this induced EMF a voltage source? No matter how it come about, as soon as you put it in the loop and start driving the circuits, it is a voltage source.

 

[stevenb]

How can you not treating this induced EMF a voltage source? No matter how it come about, as soon as you put it in the loop and start driving the circuits, it is a voltage source.

You keep side-stepping the issues with false premises on what is in disagreement. Nobody said you shouldn't treat emf as a source. But, the book used in the professor's class defines KVL to only consider potentials and says that the sum of potentials equals zero. So, both you and the Prof are saying the same thing. That is, the book is defining a version of KVL that does not apply to many cases.

So you and I and probably every one else here likes to use a definition of KVL that includes EMF in some form, while the Prof says the same, but does not call that KVL. As I said before, it's nothing but semantics, and making a big deal about anything lacking substance is a fools game.

You still have not clearly defined your KVL well enough for us to know whether you prefer the Maxwell definition, the Kraus version I posted, the MIT/Agarwal definition or some other variant. Not that it matters to me what you prefer to use, but knowing may help us to understand some of your posts better.

 

[yungman]

You keep side-stepping the issues with false premises on what is in disagreement. Nobody said you shouldn't treat emf as a source. But, the book used in the professor's class defines KVL to only consider potentials and says that the sum of potentials equals zero. So, both you and the Prof are saying the same thing. That is, the book is defining a version of KVL that does not apply to many cases.

So you and I and probably every one else here likes to use a definition of KVL that includes EMF in some form, while the Prof says the same, but does not call that KVL. As I said before, it's nothing but semantics, and making a big deal about anything lacking substance is a fools game.

You still have not clearly defined your KVL well enough for us to know whether you prefer the Maxwell definition, the Kraus version I posted, the MIT/Agarwal definition or some other variant. Not that it matters to me what you prefer to use, but knowing may help us to understand some of your posts better.

As I said before, I only concentrate on the way he did the experiment to which he made the assertion. I am not challenge the validity of any of the law. When come to EM, FL and KVL, I am still learning and don't even want to engage too heavily. I just want to make a very strong statement that what he did in the experiment was wrong, he treated the connection between the two resistor as a node or a point and he claimed that he measure different voltage from A to D and start making all the assertion of what is wrong where the very way he did the measurement was flaud. That is all I am saying. You cannot make any claim from a flaud experiment. No more, no less.

For all I care, what he claimed might be correct, but just not with this experiment. That is the one and only point I have been pushing over and over with 30 or 40 posts in this thread.

I only watched the first video where he made the claim, and I saw most of the second video to the point he show the wave form measured and I stop. All his other assertions and paper is just bla bla bla to me and I am not even interested. The experiment was wrong, and there is no point of carrying on any further. Show me an experiment I can buy, then we'll talk.

 

[stevenb]

All his other assertions and paper is just bla bla bla to me and I am not even interested. The experiment was wrong, and there is no point of carrying on any further. Show me an experiment I can buy, then we'll talk.

You've already done quite a bit of talking about an experiment you can't buy. The problem is that you claim to be right and refuse to listen to the reasons why you might be wrong. Anything that might reveal the truth looks to you like "bla bla bla". That, my friend, is the definition of arrogance.

 

[Studiot]

I really can't see how an 'experiment' can be right or wrong.

Professor Lewin did what he did. Right and wrong are value judgements and inappropriate to apply to bald facts.

In particular he assembled some apparatus, and displayed some meter readings when the meters were connected at certain points, over certain time intervals.

This is all a matter of factual record - it is neither right nor wrong.

Then we come to the matter of interpretation of the meter readings. Prof Lewin discusses these in terms of certain theories.

This part of the process can be open to interpretation and is a proper matter for discussion in this thread.

A clear and unambiguous statement of these theories helps the discussion no end.

I think I have made my position quite clear as regards to my version of these theories and to my interpretation of the facts presented.

I also afford Prof Lewin the respect due to a person who has done enough to make Professor at MIT, which must be considerable, even if I differ on some point or another.

It has already been pointed out that Kirchoff was developed for steady state conditions. So to try to apply it to a circuit where the loop EMF is decaying with time is worthy of proper discussion, and not an easy task. In particular the introduction of the time variable makes the definition of any 'voltage drop' difficult to say the least.

What do you mean by PD ? Is there a difference between Potential Drop and Potential Difference?

 

[yungman]

You've already done quite a bit of talking about an experiment you can't buy. The problem is that you claim to be right and refuse to listen to the reasons why you might be wrong. Anything that might reveal the truth looks to you like "bla bla bla". That, my friend, is the definition of arrogance.

Now we have a discussion here. I don't think you really responed to all my posts directly before. Now that I finally get your attention, let's just talk about the experiement first to establish the validity of the whole thing. Please don't call me arrogant, I am very careful not to call anyone on this forum here anything, this is a usually a rule in any forum. I called the professor because he is not in this forum. If he were to be on this forum, I would have address to him directly. I think we are too educated to call each other to the face here, please move on.

So you think the experiment was done right, and he was right to claim that point A and point D is only a point, that the voltage you measure from A to D through the 100 ohm resistor is different from D to A through the 900 ohm resistor?



BTW, I know about

$$\vec E = -\nabla V -\frac{\partial \vec A}{\partial t}$$

That in varying magnetic field, E is not conservative, that

$$\int_c \vec E \cdot d\vec l$$

is no longer path independent where the professor is driving. I know all that and that is not even in question.

 

[yungman]

I really can't see how an 'experiment' can be right or wrong.

Professor Lewin did what he did. Right and wrong are value judgements and inappropriate to apply to bald facts.

In particular he assembled some apparatus, and displayed some meter readings when the meters were connected at certain points, over certain time intervals.

This is all a matter of factual record - it is neither right nor wrong.

Then we come to the matter of interpretation of the meter readings. Prof Lewin discusses these in terms of certain theories.

This part of the process can be open to interpretation and is a proper matter for discussion in this thread.

A clear and unambiguous statement of these theories helps the discussion no end.

I think I have made my position quite clear as regards to my version of these theories and to my interpretation of the facts presented.

I also afford Prof Lewin the respect due to a person who has done enough to make Professor at MIT, which must be considerable, even if I differ on some point or another.

It has already been pointed out that Kirchoff was developed for steady state conditions. So to try to apply it to a circuit where the loop EMF is decaying with time is worthy of proper discussion, and not an easy task. In particular the introduction of the time variable makes the definition of any 'voltage drop' difficult to say the least.

What do you mean by PD ? Is there a difference between Potential Drop and Potential Difference?

There is no right or wrong in the experiment itself. But together with the statement he made about conservative and non conservative using the experiment is wrong. As I said here, context is everything. You cannot use this experiment to prove conservative or non conservative.

I thought you use PD as potential difference. I have to say I never really think too hard about the difference between potential difference and emf, their origin of where they come from. If it is there, I count it as volt, whether it is induced into the loop in this case or put a battery in between the loop.

 

[stevenb]

I don't think you really responed to all my posts directly before.

I didn't respond to many of your post because you are so far off base I don't know where to begin on many of them. I did address your critical comments about emf on the wire and why this does not show up in the measurement and why this is the reason that the measurements nodes behave as nodes, but since everything beyond the experiment is "bla bla bla" you didn't notice that or understand the significance of what I said.

By the way, I'm not calling you arrogant. I just observed that some of your actions here fit the definition of arrogance. Other actions or yours seem to say you are not arrogant, so I can't really say one way or the other without knowing you. The experiment is there to display the theory, so you can't ignore the theory and say that you haven't even tried to understand it and call it "bla bla bla" and expect to be taken seriously. Claiming you're right while dismissing the very information that is critical to understand the deeper issue is just not acceptable in a discussion like this. I just think it's ironic that you call the Professor arrogant and yet ignore his detailed analysis. You don't offer any detailed analysis yourself and you don't show us where he is wrong. All you do is argue things that we already know and then claim the experiment is wrong. Then you post pointless theory on Lorentz force and give diagrams that have nothing to do with the discussion and show total incompetence on a theoretical level.

So you think the experiment was done right, and he was right to claim that point A and point D is only a point, that the voltage you measure from A to D through the 100 ohm resistor is different from D to A through the 900 ohm resistor?

Yes, the experiment was done correctly by all evidence that we have access to. As I mentioned above, you have not provided any analysis to show where it is wrong. His measurements obey Faraday's Law, while what you claim does not obey Faraday's Law. I dont' expect you to see that because although you claim to understand FL and seem to understand FL, you don't seem able to apply it to this situation correctly and see why he is right and you are wrong.

You keep worrying about the emf on the wire which you are correct to point out is there. You fail to recognize that his measurements that do not encircle flux change will not see the wire emf because it is canceled by an equal and opposite emf on the measurement probes. For this reason, you can slide the probe connection along that 4-6 inch length of wire that you are concerned about. This is also the reason why each meter reads a different potential. One correctly reads the potential on one resistor and the other correctly reads the potential on the other resistor.

 

[stevenb]

I have to say I never really think too hard about the difference between potential difference and emf, their origin of where they come from. If it is there, I count it as volt, whether it is induced into the loop in this case or put a battery in between the loop.

This is a major failing on your part. The fact that you can admit to this and not even realize that it reveals that your theoretical understanding of the physics is not even at a basic level speaks volumes on why you are so confused on this issue. Experiments without understanding are pointless.

 

[cabraham]

Yungman, please re-read your statements about the direction of E. TEM wave prop is in the z direction, we both agree on that. We both agree that this space wave is TEM. So if power is traveling along z axis, then E & H are normal to each other & mutually normal to the z axis. Thus E & H are in the x-y plane, normal to each other.

The loop is also in the x-y plane. When all charges in the resistors & conductors are at rest, an H field cannot move them since mag fields can only exert force on moving charges. To get these charges moving, an E field is required. Said E field must be in x-y plane tangential to the loop to move charge. The point of conflict seems to be how to associate E with H. I've already pointed out that E & H are normal in the x-y plane where the loop resides. Again, if the loop were removed from the vicinity where the TEM wave is located, there is still an E & an H field in the x-y plane.

Is H inducing E, or vice-versa? We get right back to a chicken & egg vicious circle. These forums have countless threads where this & similar issues perpetuate ad infinitum. E does not "induce" H, & vice-versa. When the loop is immersed into the TEM space wave, the H cannot move the charges since they are still. But the E field can. This E field per FL exerts a force on charges per Felec = q*E. This is Lorentz' law.

But the force will result in motion & once the charges are moving, the H field, which is normal to the charge velocity, exerts a force as well per Fmag = q*(u X B). The total force is F = Felec + Fmag = q*(E + u X B).

Again, under time changing conditions, i.e. the "ac" domain, E & H are Siamese twins as they only travel together. They are 2 arms on the same beast, 2 sides of the same coin, 2 domains of the same energy, etc. The phrase "induction" is used quite loosely. The E field which motivates the charges to move, is joined at the hip with its twin, the H field. Faraday & Lorentz both apply w/o exception.

As far as the lumped parameter emf source being added to the equiv circuit, vs. the distributed parameter version, both give the right answer. But the prof point is all important. I stated earlier that in order to add the emf source into the equiv circuit, we must know its value. To do that we must measure the sum of the voltage drops across each resistor in the loop.

This sum will not always equal zero. The measured non-zero value can then be added into the equiv circuit as an independent voltage source. Then, the sum of voltages around a loop does indeed equal zero.

In order to draw the lumped equiv circuit, you must measure the sum of voltages around the distributed loop, which is usually non-zero. So the distributed circuit non-zero measured value provides the correct value for the included voltage source.

This is way too long, & we've covered it all. No debate is needed, since all phenomena are accounted for. I'll clarify if needed. BR.

Claude

 

[yungman]

I didn't respond to many of your post because you are so far off base I don't know where to begin on many of them. I did address your critical comments about emf on the wire and why this does not show up in the measurement and why this is the reason that the measurements nodes behave as nodes, but since everything beyond the experiment is "bla bla bla" you didn't notice that or understand the significance of what I said.

By the way, I'm not calling you arrogant, I just observed that some of your actions here fit the definition of arrogance. Other actions or yours seem to say you are not arrogant, so I can't really say one way or the other without knowing you. The experiment is there to display the theory, so you can't ignore the theory and say that you haven't even tried to understand it and call it "bla bla bla" and expect to be taken seriously. Claiming you're right while dismissing the very information that is critical to understand the deeper issue is just not acceptable in a discussion like this. I just think it's ironic that you call the Professor arrogant and yet ignore his detailed analysis. You don't offer any detailed analysis yourself and you don't show us where he is wrong. All you do is argue things that we already know and then claim the experiment is wrong. Then you post pointless theory on Lorentz force and give diagrams that have nothing to do with the discussion and show total incompetence on a theoretical level.


1) Cabraham brought up the Lorentz and I responded to that, that show you really not reading very carefully.
2) So you think his point D is just a point?



Yes, the experiment was done correctly by all evidence that we have access to. As I mentioned above, you have not provided any analysis to show where it is wrong. His measurements obey Faraday's Law, while what you claim does not obey Faraday's Law. I dont' expect you to see that because although you claim to understand FL and seem to understand FL, you don't seem able to apply it to this situation correctly and see why he is right and you are wrong.
Did you read #153, it is one of the post I said and I have said repeatly that this is Faraday's Law issue. I think I must have close to 5 or 6 posts saying that this experiment is about Faraday's law. Please go back and read it first, find the post that I claimed that this does not obey Faradays Laws. If you read carefully, you would find I only said Lorentz law don't apply in my discussion with Cabraham.


You keep worrying about the emf on the wire which you are correct to point out is there. You fail to recognize that his measurements that do not encircle flux change will not see the wire emf because it is canceled by an equal and opposite emf on the measurement probes.


1) If you look at the size of the round thing shown in the second video, you know that the two resistors are connect through wires, do you agree?
2) Please look at the attachment in #123 that I posted. Ignor the probe setup, The loop that the professor made must be something like that in order to cover the area of that size. In the diagram, you see there is wire between B and C and that is part of the loop that generate most of the emf that drive the resistor. Point B and point C was lumped together by the professor and called a POINT D. This is the first thing that is wrong.

For this reason, you can slide the probe connection along that 4-6 inch length of wire that you are concerned about. This is also the reason why each meter reads a different potential. One correctly reads the potential on one resistor and the other correctly reads the potential on the other resistor.

No I don't concern on the mearsuring, you are an engineer, you know how to do common mode rejection and get a good enough measurement. I am concern about the professor treating the wire between point B and C as a single node and was called D in his video.

 

[yungman]

Yungman, please re-read your statements about the direction of E. TEM wave prop is in the z direction, we both agree on that. We both agree that this space wave is TEM. So if power is traveling along z axis, then E & H are normal to each other & mutually normal to the z axis. Thus E & H are in the x-y plane, normal to each other.

The loop is also in the x-y plane. When all charges in the resistors & conductors are at rest, an H field cannot move them since mag fields can only exert force on moving charges. To get these charges moving, an E field is required. Said E field must be in x-y plane tangential to the loop to move charge. The point of conflict seems to be how to associate E with H. I've already pointed out that E & H are normal in the x-y plane where the loop resides. Again, if the loop were removed from the vicinity where the TEM wave is located, there is still an E & an H field in the x-y plane.

Is H inducing E, or vice-versa? We get right back to a chicken & egg vicious circle. These forums have countless threads where this & similar issues perpetuate ad infinitum. E does not "induce" H, & vice-versa. When the loop is immersed into the TEM space wave, the H cannot move the charges since they are still. But the E field can. This E field per FL exerts a force on charges per Felec = q*E. This is Lorentz' law.

But the force will result in motion & once the charges are moving, the H field, which is normal to the charge velocity, exerts a force as well per Fmag = q*(u X B). The total force is F = Felec + Fmag = q*(E + u X B).

Again, under time changing conditions, i.e. the "ac" domain, E & H are Siamese twins as they only travel together. They are 2 arms on the same beast, 2 sides of the same coin, 2 domains of the same energy, etc. The phrase "induction" is used quite loosely. The E field which motivates the charges to move, is joined at the hip with its twin, the H field. Faraday & Lorentz both apply w/o exception.

As far as the lumped parameter emf source being added to the equiv circuit, vs. the distributed parameter version, both give the right answer. But the prof point is all important. I stated earlier that in order to add the emf source into the equiv circuit, we must know its value. To do that we must measure the sum of the voltage drops across each resistor in the loop.

This sum will not always equal zero. The measured non-zero value can then be added into the equiv circuit as an independent voltage source. Then, the sum of voltages around a loop does indeed equal zero.

In order to draw the lumped equiv circuit, you must measure the sum of voltages around the distributed loop, which is usually non-zero. So the distributed circuit non-zero measured value provides the correct value for the included voltage source.

This is way too long, & we've covered it all. No debate is needed, since all phenomena are accounted for. I'll clarify if needed. BR.

Claude

You put in a lot of materials, I'll read throught and really think about this before responding hopefully by tomorrow. Thanks

Alan

 

[stevenb]

I am concern about the professor treating the wire between point B and C as a single node and was called D in his video.

Being concerned is fine, but you have failed to show a good reason why approximating the wire as a node has any significant effect on his analysis. I can take any circuit design ever produced and claim that every node on the drawing is not truly a node. So, your comment is a red herring. If you want to get nit-picky then it's not correct to call it a node. But, do an analysis and post the numbers that you think are in play. Just as you were originally wrong about the significance of the wire inductance, you are wrong that the wire "transformer" emf enters into any measurement that does not encircle flux change. The wire emf is in fact significant, although the potential drop on the wire is insignificant. In this case the distinction is absolutely critical because this so-called circuit does not obey a critical assumption of usual circuit theory because that emf is there. A potential drop is measurable, but the emf of this type is not measurable in any loop that does not encircle a flux change. If it were, then Faradays law would fail in the measurement loop. So, if we can move the connection point anywhere along the wire and get the same reading, that wire is effectively a node in a Faraday Law analysis. The topology relative to encirclements of flux change is the important thing here, not physical lengths for connections along the wires.

Again, you need to do more than complain and claim. You need to demonstrate with experiment or with analysis. The OP at least started on the experiment path, which I respect very much, but we still do not have his results in any form than can be scrutinized, analyzed and reproduced. If he eventually posts results along the lines he thought he was seeing, I will show him how his measurements are inconsistent with Faraday's law. He would then have to explain this failing. You are in a position to post a full analysis with schematic, identified nodes, scope connections and "claimed" voltage readings on the scopes. If you do this, I will show you why Faraday's law is not upheld in your analysis. Then you will have to explain this failing, and then we would have to see if I could poke holes in that. This is how a productive discussion can be held. You telling us 15 different ways that "he is wrong and I am right" just doesn't cut it. He did the experiment and provided an analysis, while you've done neither.

 

[yungman]

Being concerned is fine, but you have failed to show a good reason why approximating the wire as a node has any significant effect on his analysis. I can take any circuit design ever produced and claim that every node on the drawing is not truly a node. So, your comment is a red herring. If you want to get nit-picky then it's not correct to call it a node. But, do an analysis and post the numbers that you think are in play. Just as you were originally wrong about the significance of the wire inductance, you are wrong that the wire "transformer" emf enters into any measurement that does not encircle flux change.
Which part of the wire forming the loop that the flux go through in the middle of the loop like the drawing the professor had in the first video you don't understand? That the loop encircle the flux change that you don't see?
The wire emf is in fact significant, although the potential drop on the wire is insignificant. In this case the distinction is absolutely critical because this so-called circuit does not obey a critical assumption of usual circuit theory because that emf is there.
This is what I proposed to look at this as a superposition of two circuit, one is the resistor voltage drop due to current passing through, the other is the emf generated along the closed loop. I have no way to do the experiment and Sarumonkee said he was going to do it with the resistor setup I proposed in #134. I don't claim I have the answer, I just suspect the experiment will not yield the normal voltage divider ratio because it is superpositon of the FL induced emf along the loop and the voltage drop across the resistors.
A potential drop is measurable, but the emf of this type is not measurable in any loop that does not encircle a flux change. If it were, then Faradays law would fail in the measurement loop. So, if we can move the connection point anywhere along the wire and get the same reading, that wire is effectively a node in a Faraday Law analysis. The topology relative to encirclements of flux change is the important thing here, not physical lengths for connections along the wires.It is the loop encircling the flux in his experiment. Again which part of his drawing on his first video to replace the battery with a short and pulse a magnetic field through the middle between the two resistor you don't understand? You do know he is trying to use the two resistors to form a loop. And my argument is there is no way he can form a loop with just two resistors without having wires to connect the two resistors to form a loop big enough in his second video. I hope you get at least that much before you calling me wrong.

Again, you need to do more than complain and claim. You need to demonstrate with experiment or with analysis. The OP at least started on the experiment path, which I respect very much, but we still do not have his results in any form than can be scrutinized, analyzed and reproduced. If he eventually posts results along the lines he thought he was seeing, I will show him how his measurements are inconsistent with Faraday's law. He would then have to explain this failing. You are in a position to post a full analysis with schematic, identified nodes, scope connections and "claimed" voltage readings on the scopes. If you do this, I will show you why Faraday's law is not upheld in your analysis. Then you will have to explain this failing, and then we would have to see if I could poke holes in that. This is how a productive discussion can be held. You telling us 15 different ways that "he is wrong and I am right" just doesn't cut it. He did the experiment and provided an analysis, while you've done neither.

Did you read #90, that Sarumonkee did the experiment and saw the voltage on the wire? He did see the 9:1 ratio on the resistors. He grounded both probe grounds in the middle of the loop and measure the two end of the wire which I called point B and C. He measure equal and opposite voltage. Then he move the probe around verticle and horizontal to prove the reading is consistence. Which part of this you don't understand?

You cannot blanketly said the ground lead of the probe with cause a loop and pickup the flux no matter what. I hope you do understand that the area of any loop has to ENCIRCLE the flux in order for the loop to have induced emf. That the flux pattern of that set up is very predictable. Call the loop on xy plane, flux in +z direction, the flux will start bending and eventually going at -z direction and curl back to the other end of the flux generator. Or you just think you can shot down his finding no matter what!?

You follow? And if you move the probe and the ground lead so the loop formed by the probe is verticle or horizontal to the xy plane, flux enclosed will be different.You follow so far?

As I said, I did not see Saru's experiment, but by moving the probe in all different position and not seeing any change can tell you that there are at least voltage across the wire.

So you still say the wire is just one node D and need to proof more on this? BTW, what engineering field are you in?

In case you don't get it:

I show the flux pattern and you can see the area of the loop formed by the probe in green for verticle and red in horizontal. You don't get the same amount of flux through the loop in different position. And the flux will not be anywhere close to the flux through the circuit loop unless you intentionally make the loop of the probe onto the middle of the set up, and this is asking for it.

 

[stevenb]

there are at least voltage across the wire.

So you still say the wire is just one node D and need to proof more on this? BTW, what engineering field are you in?

Why do you belabor what is already known and accepted? Yes, there is at least voltage across the wire. This voltage is a good chunk of the loop emf. I already said that the emf is there in agreement with you. There are no arguments about this. If this, to you, means that node D is not a real node, then don't consider it a node. What do I care what you call it? Again, it's semantics. The issue is, what do you do with this wire with emf on it. With Faraday's Law, you don't have to think about it at all. With measurements, you won't see it if your measurement loop does not enclose flux. Why? Because Faraday's Law says so.

I really don't want to go through all your comments. You state many things that I know and accept, and I don't see the point of going through it. There is only one issue here. You still have not explained how a measurement loop that does not encircle any flux, has emf from the wire and an equal and opposite emf on the scope wires, and yet reads the wire emf. That violates Faraday's Law. How Sarumonkee made a measurement that violates Faraday's law is beyond my explanation because I wasn't there to witness it and see cross checks and verifications. I agree with his conclusion that there is emf on the wire, but I don't understand how the measurement revealed this.

What I can say is that after the holidays I'll bite the bullet and do the measurement with cross-checks and analysis and post it. Until then, I'll wait to see if something substantial in the form of checkable experimental results or an actual analysis comes forth.

 

[Born2bwire]

Yes I did look. For a transmission line (2 wire, parallel or coax), the wave propagates in TEM (transverse electromagnetic) mode. So does a space wave. But for a waveguide, TE (transverse electric) & TM (transverse magnetic) modes exist, no TEM mode at all takes place.

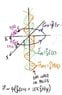
For TEM mode, if wave propagation is along z axis, then E is in x axis, & H is in y axis, or any orientation in x-y plane normal to each other. For TE mode, propagation remains along z axis, E is in x axis, but H is in y-axis & z axis. E is transverse (normal) to prop, but H has 2 components, 1 normal to prop, & 1 coincident with prop. So if wave prop is in z axis, E is in x axis, H is in y & z axes. Only E is transverse to prop direction.

For a TM it's vice versa. So in Prof. Lewin's setup, only the TEM mode takes place. If energy is propagating in z direction, then E & H/B are normal to each other in x-y plane, as well as normal to prop.

"Inducing" an E field into the loop is a colloquial phrase. This E field is present in space regardless of whether or not the loop is there. H & E cannot exist independently under time changing conditions. Sorry to be late responding. Christmas season, shopping, fixing up the house, you know.

Claude

I would clarify though that even in a waveguide the actual wave is TEM (though I'm sure somebody here knows of some kind of rare exception to this case). When we speak of TE and TM modes we are talking in reference to the GUIDED direction of propagation. The actual wave does not actually travel in the guided direction but it bounces back and forth off of the geometry of the waveguide such that the net direction of propagation is along the guided direction. A subtle clarification but I have seen it lead to misunderstanding regarding the situations where you can truly get a non-TEM mode (which is generally restricted to more esoteric situations like surface waves in inhomogeneous media).

As for some previous points about Faraday's Law and the Lorentz force, the two are inseparable. Anytime that you have an induction of current or potential difference this is always done via the Lorentz force since the Lorentz force is the mechanism by which the fields interact with charges and currents. Faraday's Law implicitly includes the effects of the Lorentz force (as do the other laws) when it relates the creation of an EMF via a flux (and this is shown explicitly in just about any given textbook in some basic examples).

It should also note that Faraday's Law incorporates this via two different mechanisms. The first mechanism is due to the motion of the circuit physically through a spatially varying magnetic field (in which case by moving the circuit we provide moving charges). The second mechanism is due to the fact that a time-varying magnetic field always means that we have an associated time-varying electric field. This electric field can provide a Lorentz force on stationary charges which is given as the EMF.

 

[yungman]

Why do you belabor what is already known and accepted? Yes, there is at least voltage across the wire. This voltage is a good chunk of the loop emf. I already said that the emf is there in agreement with you. There are no arguments about this. If this, to you, means that node D is not a real node, then don't consider it a node. What do I care what you call it? Again, it's semantics. The issue is, what do you do with this wire with emf on it. With Faraday's Law, you don't have to think about it at all. With measurements, you won't see it if your measurement loop does not enclose flux. Why? Because Faraday's Law says so.
why is that you don't look at the induced emf on the wire in the loop as part of the loop that we use Faraday's law to calculate the emf? I am absolutely confuse on this point. Why is the problem is not that simple as the wire have the induced voltage that drive the two resistor and and get the 9:1` ratio on the voltage? Far as I concern, you go through the whole loop and the voltage end up to be zero as KVL said. It is good for either direction.
I really don't want to go through all your comments. You state many things that I know and accept, and I don't see the point of going through it. There is only one issue here. You still have not explained is how a measurement loop that does not encircle any flux, has emf from the wire and an equal and opposite emf on the scope wires,

Which wire specificly you talked about that does not encircle any flux where I put the bold fonds on above?
This is the copy of Sarumonkee on post #90 in case you have not read it:

I observed a factor of about 1:9 as expected in the two voltages, since this was the ratio of the resistances. Now, the fun part. I connected the grounds of the probes to half way between the long wire, about 3" from both resistors, leaving the probe ends in the same location. Since this is a "node" in Lewin's analysis, I should not see any voltage across it if I make another step function on the primary.

Well, I introduced my step, and both probes read about the same magnitude (one was negative from the other, since it points the other way), and the sum of the two magnitudes (had to invert one because I wasn't using differential probes) equaled the sum of the previous points in standard KVL style, all adding to 0 if you do the loop. I was measuring a voltage across the 6" wire in two 3" segments.

I also held the probes above, across, and in many different orientations, and it still produced the same results. I plan on taking some pictures and maybe making a video this weekend if I have time.

What he was doing is putting the scope ground at the mid point of the 6" wire that connect the two resistors. He put one probe on one end and the other on the other end of the wire. Essentially he take the mid point of the wire as a reference and look at the voltages induced on both end of the wire and it was found equal and opposite. Does that mean anything to you? He actually went out of his way to move the probe up and down and every position to show the reading did not change to prove the probe loop did not significantly alter the reading. Have you stop and think about this? He did a very very good job and the result cannot be more clear that the voltage exist on that wire and that was the voltage that drive the two resistors. Plane and simple.


and yet reads the wire emf. That violates Faraday's Law. How Sarumonkee made a measurement that violates Faraday's law is beyond my explanation because I wasn't there to witness it and see cross checks and verifications. I agree with his conclusion that there is emf on the wire, but I don't understand how the measurement revealed this.

No, what he did did not violate the FL, in fact he proof the FL is in play here. That the voltage was induced into the loop and create a voltage source. AND if you take into account of the voltage, KVL apply perfectly.

What I can say is that after the holidays I'll bite the bullet and do the measurement with cross-checks and analysis and post it. Until then, I'll wait to see if something substantial in the form of checkable experimental results or an actual analysis comes forth.

If you can look at the drawing that I provided in #134 and Sarumonkee said he was going to try last week, I have a suspicion that you are not going to get the predicted voltage ratio across each resistor like 0.9V on the 900ohm. And don't say v=IR fail! I think you have to look at it as super-position of two event...1) voltage from the current passing through the resistors and 2) the induced emf onto the loop made up of the resistors. In this case, there are very little wire, the body of the loop made up of resistor material. I suspect the voltage source induced are distributed inside the resistors and make the reading different from prediction of V=IR. I am not absolutely sure, just a thought. But this will proof the point that if you consider induced emf as a voltage source, KVL work perfectly.

In my book, that prove the point. You have to care about what voltage induced along the wire.

To be sure you know what I am talking about, this is the picture. The wire is between point B and C which the professor call it a node or point D. As shown in red, the ground of the two probes attached in the middle 3" from B and from C and the probe measure point B and C which I called Probe B and Probe C. The professor claimed he measure 0.1 on the 100 ohm and 0.9 on the 900ohm. Of cause, I never disagreed, it is the wire from B to C. As in the drawing,

 

[yungman]

Yungman, please re-read your statements about the direction of E. TEM wave prop is in the z direction, we both agree on that. We both agree that this space wave is TEM. So if power is traveling along z axis, then E & H are normal to each other & mutually normal to the z axis. Thus E & H are in the x-y plane, normal to each other.

The loop is also in the x-y plane. When all charges in the resistors & conductors are at rest, an H field cannot move them since mag fields can only exert force on moving charges. To get these charges moving, an E field is required. Said E field must be in x-y plane tangential to the loop to move charge. The point of conflict seems to be how to associate E with H. I've already pointed out that E & H are normal in the x-y plane where the loop resides. Again, if the loop were removed from the vicinity where the TEM wave is located, there is still an E & an H field in the x-y plane.

Is H inducing E, or vice-versa? We get right back to a chicken & egg vicious circle. These forums have countless threads where this & similar issues perpetuate ad infinitum. E does not "induce" H, & vice-versa. When the loop is immersed into the TEM space wave, the H cannot move the charges since they are still. But the E field can. This E field per FL exerts a force on charges per Felec = q*E. This is Lorentz' law.

But the force will result in motion & once the charges are moving, the H field, which is normal to the charge velocity, exerts a force as well per Fmag = q*(u X B). The total force is F = Felec + Fmag = q*(E + u X B).
You know, I never thought of it this way, this is interesting. I don't dare to agree or disagree. I just want to present to you my understanding why E field have no effect. Take a look and tell me your feeling.

In the diagram below, I drew the loop in blue, the E of the TEM in red. Notice it is on the x-axis occilating back and fore as the red arrow pointing both ways. Induced E is opposite direction to the applied E, so I drew the orange arrow of the vector component along the loop for the +ve part of the E wave ie when the wave is moving towards the +ve x direction. As you can see, the induced E want to go both ways, one towards the CCW direction and the other go towards CW. This is shown as $\vec E_{+y} \hbox { and } \vec E_{-y}$. The result is cancellation. I am not making a strong statement here, this is just how I look at this. Please give me your feedback.

I can see your point even if the E don't keep the current flow, but it would give it a kick start and the B take over. that is a very good question on the FL that who started the motion if B cannot change the velocity. AND the motion of the electrons in the loop is random motion initially.
Again, under time changing conditions, i.e. the "ac" domain, E & H are Siamese twins as they only travel together. They are 2 arms on the same beast, 2 sides of the same coin, 2 domains of the same energy, etc. The phrase "induction" is used quite loosely. The E field which motivates the charges to move, is joined at the hip with its twin, the H field. Faraday & Lorentz both apply w/o exception.

As far as the lumped parameter emf source being added to the equiv circuit, vs. the distributed parameter version, both give the right answer. But the prof point is all important. I stated earlier that in order to add the emf source into the equiv circuit, we must know its value. To do that we must measure the sum of the voltage drops across each resistor in the loop.

This sum will not always equal zero. The measured non-zero value can then be added into the equiv circuit as an independent voltage source. Then, the sum of voltages around a loop does indeed equal zero.

In order to draw the lumped equiv circuit, you must measure the sum of voltages around the distributed loop, which is usually non-zero. So the distributed circuit non-zero measured value provides the correct value for the included voltage source.

This is way too long, & we've covered it all. No debate is needed, since all phenomena are accounted for. I'll clarify if needed. BR.

Claude

I'll look at the second half of your write up tomorrow as this is getting really late. I'll edit this post to up date. You spend the time writing this long one and I want to really read it over first.

 

[stevenb]

If you can look at the drawing that I provided in #134 and Sarumonkee said he was going to try last week, I have a suspicion that you are not going to get the predicted voltage ratio across each resistor like 0.9V on the 900ohm. And don't say v=IR fail! I think you have to look at it as super-position of two event...1) voltage from the current passing through the resistors and 2) the induced emf onto the loop made up of the resistors. In this case, there are very little wire, the body of the loop made up of resistor material. I suspect the voltage source induced are distributed inside the resistors and make the reading different from prediction of V=IR. I am not absolutely sure, just a thought. But this will proof the point that if you consider induced emf as a voltage source, KVL work perfectly.

In my book, that prove the point. You have to care about what voltage induced along the wire.

To be sure you know what I am talking about, this is the picture. The wire is between point B and C which the professor call it a node or point D. As shown in red, the ground of the two probes attached in the middle 3" from B and from C and the probe measure point B and C which I called Probe B and Probe C. The professor claimed he measure 0.1 on the 100 ohm and 0.9 on the 900ohm. Of cause, I never disagreed, it is the wire from B to C. As in the drawing,

Again, pretty pictures do not replace a full analysis. Also, stating known things that we agree on does nothing productive. You still have not answered my critical question.

It seems you don't even understand the question so I may need to use your drawing to indicate the measurement loop that violates Faraday's law. I'm on mobile now so I'll have to do that later.

I can make one more verbal attempt. Just as you say the wire emf in the main loop completes your version of KVL (not Lewin's version mind you), I can say that the scope leads themselves also have emf that completes your version of KVL. Why? Because Faraday's Law says any loop is valid, and the scope provides a new loop once you hook it up. Do you understand this point? If not, wait for my diagram. If you do understand this, then analyze the loop formed by the scope and the main wire. This loop does not encircle much flux, as you show in your diagrams. FL says that the emf in this loop is zero. Hence, I ask again, how does the scope register voltage in a loop with two equal and opposite EMFs that add to zero (or small really)? If you can answer this question then you would convince me you are right. So, I recommend you concentrate on this critical point.

EDIT: I've attached a pdf for a drawing which may make my point more clear. Note that loop 1 and loop 2 encircle the full flux change. Loop 3 does not encircle very much flux change.

 

[yungman]

Again, pretty pictures do not replace a full analysis. Also, stating known things that we agree on does nothing productive. You still have not answered my critical question.

It seems you don't even understand the question so I may need to use your drawing to indicate the measurement loop that violates Faraday's law. I'm on mobile now so I'll have to do that later.
Your drawing is wrong, you really need to read things more carefully before you write. You missed the most important thing...THE SCOPE PROBE GROUNDS IN THE MIDDLE OF THE WIRE C AND D !
I can make one more verbal attempt. Just as you say the wire emf in the main loop completes your version of KVL (not Lewin's version mind you), I can say that the scope leads themselves also have emf that completes your version of KVL. Why? Because Faraday's Law says any loop is valid, and the scope provides a new loop once you hook it up. Do you understand this point? If not, wait for my diagram. If you do understand this, then analyze the loop formed by the scope and the main wire. This loop does not encircle much flux, as you show in your diagrams. FL says that the emf in this loop is zero. Hence, I ask again, how does the scope register voltage in a loop with two equal and opposite EMFs that add to zero (or small really)? If you can answer this question then you would convince me you are right. So, I recommend you concentrate on this critical point.

EDIT: I've attached a pdf for a drawing which may make my point more clear. Note that loop 1 and loop 2 encircle the full flux change. Loop 3 does not encircle very much flux change.

The scope probe ground take to loop 3 out all together. Why? In the scope, each channel measure the DIFFERENTIAL voltage, the voltage between the probe head and it's OWN ground leads. Did you even look at my diagram that I have the ground leads on, AND Saru have detail description about the probe ground leads?

If you really want to argue the loop between the two probes. The only loop will be from E to F to the probe ground at D, then to the middle of the wire CD to the ground lead of probe at D. Then go back to E. That is not in the signal path.

BTW, there is really no internal resistance between E and F. They are of separate channel. Your resistance is differential mode resistance between the two channel.

I know most of the scope have isolated return( ground) on the probe input BNC connectors. This is to address these kind of problems.

Can you please read Saru's #90 again before we go any further? I marked up your drawing to show you what is missing and my comments.

 

[Studiot]

One point of interest here.

I note that most respondents talk about loops 'encircling' or in some way 'sourrounding' the flux.

Since the loops were there before the flux was generated and after the flux was dissipated I prefer the old fashioned view that the flux threads the loop.

When the flux changes an EMF is generated.
The loop does not change or move.

@yungman

Do you truly understand the difference between EMF and Voltage?
There is a (not so subtle) difference which has major implications although both are measured in volts.

 

[yungman]

One point of interest here.

I note that most respondents talk about loops 'encircling' or in some way 'sourrounding' the flux.

Since the loops were there before the flux was generated and after the flux was dissipated I prefer the old fashioned view that the flux threads the loop.

When the flux changes an EMF is generated.
The loop does not change or move.

@yungman

Do you truly understand the difference between EMF and Voltage?
There is a (not so subtle) difference which has major implications although both are measured in volts.

Apparently I don't think I do, can you clearify for me? I am not being sacastic here!


But what is the difference here? If there is real voltage in the loop as shown in #90, it is a voltage source. Maybe I truly missing the point. But I would like to see how the debate of Saru's experiment here pend out because the KVL around the loop is zero if you consider the emf induced into the loop.

 

[Studiot]

But what is the difference here? If there is real voltage in the loop as shown in #90, it is a voltage source. Maybe I truly missing the point. But I would like to see how the debate of Saru's experiment here pend out because the KVL around the loop is zero if you consider the emf induced into the loop.
T 05:59 PM

If you can catch my answer to this you should also be able to see the difference between EMF and Voltage.

Ask yourself: What value would you put on the EMF underlined in the quote above?

Please note this is not a trick question and doesn't need a long winded answer.

EMF and Potential are both measured in volts, but they are different.
They are not the only pairs of quantities in Physics to share a unit but be different.

For example what is measured in Newton-metres?

Answer 1) Work = Force x Distance

Answer2) Moment = Force x Distance

Are they the same?

 

[stevenb]

Can you please read Saru's #90 again before we go any further? I marked up your drawing to show you what is missing and my comments.

yungman. I read your posts and Saru's posts very carefully. I was hoping that you would see that I was only analyzing one of the scope loops and leaving the other one out of the drawing for clarity. I did not miss anything, but simply tried to keep the drawing uncluttered. Maybe you can go back and look to see that my scope is not grounded at point B, but at a midpoint. I guess I should have used the label G instead of D, but I thought it would be clear. You just have to mentally think about the other scope also being there, but its presence does not affect the application of Faraday's law on loop 3.

Whether you want to carefully consider what I tried to show is up to you, but I'm doing my best to communicate to you what I believe to be the fundamental difference between our points of view. You still don't see the violation of Faraday's law in loop3, nor do you explain why it is not a violation. You claim wire CEFD does not have emf on it, but don't explain why. I explain that it is there because using Faraday's Law on loop 2 says it should be there. This is where we disagree.

At this point, I'll just bow out of the discussion and return after I do the measurements. Going back and forth won't let us understand each other. I'll do the experiment exactly according to your diagram and we'll see what we see.

 

[yungman]

yungman. I read your posts and Saru's posts very carefully. I was hoping that you would see that I was only analyzing one of the scope loops and leaving the other one out of the drawing for clarity. I did not miss anything, but simply tried to keep the drawing uncluttered. Maybe you can go back and look to see that my scope is not grounded at point B, but at a midpoint. I guess I should have used the label G instead of D, but I thought it would be clear. You just have to mentally think about the other scope also being there, but its presence does not affect the application of Faraday's law on loop 3.
sorry, my bad, I read this one wrong. But you drawing is still not correct. The scope probe ground go directly to the probe body. Loop 3 is actually very small like what I drew in #197. And Like you said and I had diagram in #196 show that your loop 3 is outside of the main magnetic field, it only catches very limited amount of induced emf. And Saru did move around the probe and see no difference in reading. Here is his direct copy:

Well, I introduced my step, and both probes read about the same magnitude (one was negative from the other, since it points the other way), and the sum of the two magnitudes (had to invert one because I wasn't using differential probes) equaled the sum of the previous points in standard KVL style, all adding to 0 if you do the loop. I was measuring a voltage across the 6" wire in two 3" segments.

I also held the probes above, across, and in many different orientations, and it still produced the same results. I plan on taking some pictures and maybe making a video this weekend if I have time.
Notice he saw equal and opposite voltage from the two probe because the reference is at the mid point so one end is +ve and the other is -ve with equal magnitude. And he specificly said the reading is equal to the voltage of the resistors and the voltage around the whole loop is zero as KVL predicted. Please read it again before you invalidate his work.

Whether you want to carefully consider what I tried to show is up to you, but I'm doing my best to communicate to you what I believe to be the fundamental difference between our points of view. You still don't see the violation of Faraday's law in loop3, nor do you explain why it is not a violation. You claim wire CEFD does not have emf on it, but don't explain why. I explain that it is there because using Faraday's Law on loop 2 says it should be there. This is where we disagree.
I did not argue about violation of the faraday's Law! I only point out that the experiment the professor did was not supporting his claimed that because the emf is not conservative, it is path dependent and you get different reading going around the loop through the 900 resistor or the 100 resistor.
At this point, I'll just bow out of the discussion and return after I do the measurements. Going back and forth won't let us understand each other. I'll do the experiment exactly according to your diagram and we'll see what we see.

Don't make it more complicated than what it is. I only challenge the validity of his experiment to show non conservative field is path dependent. Nothing more, don't get too deep into validating FL etc. for all I know the theory he said might be right, but NOT PROVED BY HIS EXPERIMENT.

His experiment failed because Saru did his experiment and found equal voltage on the wire and if you sum around the loop, it is zero. So pick a point and go both CW or CCW, you get the same result. YES if you just measure with probe directly on the resistors, you get the 9:1 ratio in this case as Saru said.

Please explain what is the difference if the voltage is emf induced by the mag field or it is a voltage source like a battery? Isn't it that as long as you have any voltage in the loop, you count is in KVL?

 

[yungman]

If you can catch my answer to this you should also be able to see the difference between EMF and Voltage.

Ask yourself: What value would you put on the EMF underlined in the quote above?
As I predicted and verified in post #90 from Saru that it is equal to the voltage drop on the two resistors which is supposingly 1v if you consider 0.9 on the 900 and 0.1 on the 100. this is rough reading as there are also emf induced into the length of the resistor's bodies. But at rough estimate, we let the emf in the resistor be zero for the moment.
Please note this is not a trick question and doesn't need a long winded answer.
I don't consider it's a trick question. I have a lot to learn about physics. I argue the validity of the experiment to prove the point of conservative and non conservative field like the professor said in the first video. I don't even mean to get this deep. As I said way from the beginning that the wire in the loop is the difference and you cannot treat the wire as a point. No more and no less.
EMF and Potential are both measured in volts, but they are different.
They are not the only pairs of quantities in Physics to share a unit but be different.

For example what is measured in Newton-metres?

Answer 1) Work = Force x Distance

Answer2) Moment = Force x Distance

Are they the same?

If you think I am really wrong, can you please tell me what I don't see. I think at this point I really get the heavy guns' attention and if I am wrong, I am wrong. But would really want to know why people discount the reading on the wire or why it is not important. Remember I am only limited on what the professor said in the first video that if the field is non conservative, then it is path dependent and you get different measurement measuring from point A to point D in either CW or CCW direction.

 

[cabraham]

I would clarify though that even in a waveguide the actual wave is TEM (though I'm sure somebody here knows of some kind of rare exception to this case). When we speak of TE and TM modes we are talking in reference to the GUIDED direction of propagation. The actual wave does not actually travel in the guided direction but it bounces back and forth off of the geometry of the waveguide such that the net direction of propagation is along the guided direction. A subtle clarification but I have seen it lead to misunderstanding regarding the situations where you can truly get a non-TEM mode (which is generally restricted to more esoteric situations like surface waves in inhomogeneous media).

As for some previous points about Faraday's Law and the Lorentz force, the two are inseparable. Anytime that you have an induction of current or potential difference this is always done via the Lorentz force since the Lorentz force is the mechanism by which the fields interact with charges and currents. Faraday's Law implicitly includes the effects of the Lorentz force (as do the other laws) when it relates the creation of an EMF via a flux (and this is shown explicitly in just about any given textbook in some basic examples).

It should also note that Faraday's Law incorporates this via two different mechanisms. The first mechanism is due to the motion of the circuit physically through a spatially varying magnetic field (in which case by moving the circuit we provide moving charges). The second mechanism is due to the fact that a time-varying magnetic field always means that we have an associated time-varying electric field. This electric field can provide a Lorentz force on stationary charges which is given as the EMF.

But the wave is still not TEM. I know about the bouncing, as every e/m text covers it. My point was that when we measure the fields, or their consequences such as induction, we are measuring the superposition of usually more than one phenomena. The fact that a waveguide measures as non-TEM by virtue of multiple waves bouncing does not make it TEM. In other words, if we bounce a true TEM space wave within the boundaries of a waveguide, & then measure a non-TEM result, we call this "non-TEM". The reason for this being bouncing, or whatever does not change this observation.

If a TEM wave undergoes multiple internal bounces, making it "look" like TE or TM, then it is understood as being TE or TM. No need to involve more detail than necessary. The bouncing is understood & need not be elaborated upon.

My point was that we cannot assume that H is along the same direction as E, or the power prop direction z. In free space, only the TEM mode can exist. If the power is propagating in the z direction, then E & H must both lie in the x-y plane, normal to one another. This is so because only the TEM mode can exist in Dr. Lewin's setup, which is the topic at hand, not waveguides.

I mentioned that only in a waveguide can E or H occur along the same direction as the power propagation. This is TE or TM mode of operation. The fact that bouncing is responsible for this mode of operation is irrelevant. My point was that a free space wave is TEM only. That is the point being debated & clarified. The OP question is with regard to Dr. Lewin's setup, which does not involve waveguides at all.

I don't wish to appear hostile, but I ask all to stay focused on the original question, & avoid tangential info. BR.

Claude

 

[Studiot]

doesn't need a long winded answer.

Yet you supplied 8 lines to state 1 volt.

It would have been better for you to have addressed the rest of my post with all that effort, we could proceed at a much faster rate that way.

Yes indeed did not Prof Lewin state explicitly that he had arranged first his battery and then his coil to supply/induce exactly 1 volt?

 

[yungman]

Yet you supplied 8 lines to state 1 volt.

It would have been better for you to have addressed the rest of my post with all that effort, we could proceed at a much faster rate that way.

Yes indeed did not Prof Lewin state explicitly that he had arranged first his battery and then his coil to supply/induce exactly 1 volt?

Then why did he claimed the measurement CW and CCW is different if he take the induced emf into consideration. Is he not consider point D a note rather a piece of wire?


You gave the answer and I see what you are driving, what is the point of reply? Why don't you give me the difference between emf and potential difference...voltage? Here I am concerning with the measured voltage along the loop and whether you call it emf or voltage, do you agree the sum around the loop is zero?


As I repeated so many times, if the professor acknowledge that 1V is induced into the loop, why then he go around the loop as if the voltage is not there. If it is so obvious the the wire have the induced volt, why he discount the wire as just a note. You people keep accusing me of repeating this over and over, then why in the 10+ pages, no body directly answer this really really simple question? I have to resort to insulting the professor repeatly to finally get direct response now...after 10+ pages.


I get that you people totally discount the emf, but my question is why? Do you not look at the real world measurement or you just worry ONLY about the definition on paper? What did I miss?

 

[Studiot]

I am offering to take this through from first principles to a fruitful discussion about Lewin's experiment.

If you do not want to do this let us abandon it now.