Is my approach for pascal's law wrong?

[Dileep Ramisetty]

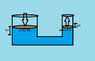
In hydraulic lift utilising pascal law, larger piston area is A1 and the smaller piston area is A2
mass in = mass out and volume in = volume out (in-compressible),so
A1*x1=A2*x2 (let x1 and x2 are displacements of respective pistons)
A1*V1 =A2*V2 (on differentiation gives continuity eq)
A1 * acceleration1=A2*acceleration2 (on differentiating again)
as mass flow rates m are equal,
m*A1*acceleration1=m*A2*acceleration2
A1*F1=A2*F2 (is giving me inverse of the pascal law)
please clarify...Thank you

 

[mfb]

m*a₁ is not the force on plate 1, no matter what "m" is.
m*a₂ is not the force on plate 2, no matter what "m" is.

In particular, you can have a force without any acceleration.

Typically those problems assume that the acceleration is small and can be neglected. Otherwise Pascal's law needs modifications.