hunter45
- 7
- 0
I have this question from another site where a member asked this. I attempted to answer it and they think it is incorrect. I would therefore like someone who knows what they are talking about to answer this question if it is incorrect and explain where I am going wrong. Thank you.
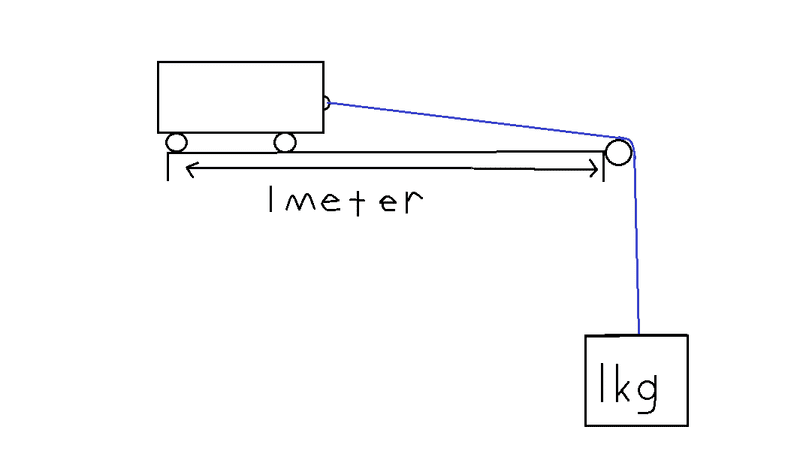
Question : How long will it take to travel that 1 metre?
NOTE: The surface is a frictionless surface. The mass of the trolley is 0.5kg
My method:
F = ma , F = (0.5+1) X 9.8 = 14.7N
W= Fd , W = 14.7 X 1 = 14.7J
Ek = 1/2mv^2
14.7 = 0.5 X 1.5 X v^2
v^2 = 19.6, v = 4.427 m/s
v = d/t
t = d/s
t = 1/4.427
t = 0.226s
Question : How long will it take to travel that 1 metre?
NOTE: The surface is a frictionless surface. The mass of the trolley is 0.5kg
My method:
F = ma , F = (0.5+1) X 9.8 = 14.7N
W= Fd , W = 14.7 X 1 = 14.7J
Ek = 1/2mv^2
14.7 = 0.5 X 1.5 X v^2
v^2 = 19.6, v = 4.427 m/s
v = d/t
t = d/s
t = 1/4.427
t = 0.226s