Is Net Charge Conserved in Special Relativity with Current Flowing in a Wire?

[arpon]

Consider an infinite wire that has no electric current initially.

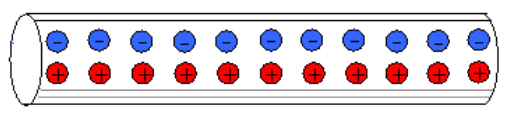
Then current starts to flow in the wire, i.e. the free electron drifts at speed $v$ (and the positive charges are fixed)
Applying special relativity, it appears that the distance between the electrons shrinks, i.e, density of electron in the wire increases.

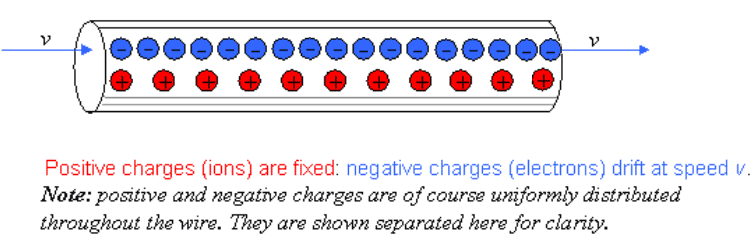
So, it seems to me that the net charge is not conserved in this case, as the negative charge density has increased.

 

[Orodruin]

What makes you think the distance between the electrons in their rest frame is the same?

 

[arpon]

What makes you think the distance between the electrons in their rest frame is the same?

Thanks for your reply. At first, it seemed very obvious to me. Later on, when I thought whether the distance should be same or not and why, I couldn't reason it out. Would you please give me some clue?

 

[Orodruin]

Your argumentation in the first post should already tell you that the distance between the electrons in their rest frame is different in the two scenarios if you want an uncharged conductor carrying a current.

However, there will be inertial frames where the conductor is negatively or positively charged. This follows from the Lorentz transformation of the 4-current.

 

[arpon]

Your argumentation in the first post should already tell you that the distance between the electrons in their rest frame is different in the two scenarios if you want an uncharged conductor carrying a current.

However, there will be inertial frames where the conductor is negatively or positively charged. This follows from the Lorentz transformation of the 4-current.

And in these inertial frames, the wire will always be negatively or positively charged (when any extra charge is not added to the system). The net charge will be conserved in a particular reference frame, but may vary from one frame to another.
As, there is no absolute reference frame, we cannot determine the 'absolute' net charge of the universe.
Do you agree with me?

 

[Orodruin]

And in these inertial frames, the wire will always be negatively or positively charged (when any extra charge is not added to the system). The net charge will be conserved in a particular reference frame, but may vary from one frame to another.
As, there is no absolute reference frame, we cannot determine the 'absolute' net charge of the universe.
Do you agree with me?

Your argumentation assumes that this wire is infinite. This leads to a distribution of matter not going to zero at infinity and it is unclear how you want to start a current in an infinite wire (this would actually take an infinite amount of time).

 

[arpon]

Your argumentation assumes that this wire is infinite. This leads to a distribution of matter not going to zero at infinity and it is unclear how you want to start a current in an infinite wire (this would actually take an infinite amount of time).

Does it matter?

 

[Orodruin]

Yes. The way to determine the total charge would be to integrate the charge density over all of space. If the charge density is not a function which decays sufficiently fast, this integral becomes nonsense.

 

[Dale]

To follow on with what Orodruin said, for a realistic scenario without an infinite wire (i.e. a circuit with a current loop), you do wind up with charge conservation. The charge density increase on one side of the circuit will be offset by a charge density decrease on the other side.

 

[pervect]

You didn't really specify what made the charges flow. If we assume that the charges flow because you applied a battery, and we additionally apply Maxwell's equations, we know that charge will be conserved, because a battery can't generate or destroy charges, it can only make them flow, and Maxwell's equations require charge conservation.

Applying Maxwell's equations to a current loop in free space is rather complex, it's much simpler if you have the wire over a ground plane, or some other system such as a pair of wires that acts as a transmission line. Charge will still be conserved either way, but it's a lot harder to analyze analytically what happens by applying Maxwell's equations - I don't think I've ever seen it done in the literature.

If you do do the transmission line analysis, you basically find that charge conservation does apply as expected, and that the assumption that the charges kept a constant proper distance when they started moving is wrong, at least when the charges are made to move by a battery.

It doesn't really matter whether you analyze a finite transmission line or an infinite one, but you do need to clarify the details of what makes the charges flow to analyze sensibly what happens. And you also need to consider the time element, how and when the charges start to move in a physically realilstic manner, if you want physically realistic results. Having all the charges "magicaly" start moving at the same time isn't physicall, having the charges flow as a pulse through a transmission line is.

AFAIK, if you have a current loop generated by a battery, you won't see any redistribution of charge from the viewpoint of a stationary observer, but you may and will see charge redistribution from the frame of reference of a moving observe. This is basically Purcell's analysis of the magnetic field.

 

[Fantasist]

The charge density increase on one side of the circuit will be offset by a charge density decrease on the other side.

How can that be if the current loop is at rest (which the OP seemed to be implying)? The length contraction factor should be the same around the loop.

 

[Dale]

How can that be if the current loop is at rest (which the OP seemed to be implying)?

It is not at rest in the frames where the charge density changes.

The length contraction factor should be the same around the loop.

Remember, length contraction is only occurs in the direction parallel to the motion, not in all directions.

 

[Ibix]

How can that be if the current loop is at rest (which the OP seemed to be implying)? The length contraction factor should be the same around the loop.

The electrons are moving with respect to the loop - one direction on one side of the loop and the other direction on the other side. That means that there is no frame in which they are all at rest, and in any frame except the rest frame of the loop they have different speeds and hence different gammas.

 

[Fantasist]

That means that there is no frame in which they are all at rest, and in any frame except the rest frame of the loop they have different speeds and hence different gammas.

We are considering the rest frame of the loop. Consider a circular super-conducting loop where initially all electrons are rest. The OP was asking what happens if all electrons are set somehow in motion. Would a resulting increased electron density throughout the loop not violate charge conservation?

 

[Ibix]

We are considering the rest frame of the loop. Consider a circular super-conducting loop where initially all electrons are rest. The OP was asking what happens if all electrons are set somehow in motion. Would a resulting increased electron density throughout the loop not violate charge conservation?

Why would there be an increased electron density in that frame? That there is not is the point Orodruin made in posts #2 and #4.

 

[Dale]

We are considering the rest frame of the loop.

Post 1 was considering the rest frame of the wire. Post 4, 5, and on were considering other frames.

 

[A.T.]

Would a resulting increased electron density throughout the loop not violate charge conservation?

It would, that's why it doesn't happen in the rest frame of the loop.

 

[Fantasist]

Why would there be an increased electron density in that frame? .

Maybe because of the length contraction effect? You can find it explained in many educational resources, for instance in http://physics.weber.edu/schroeder/mrr/MRRtalk.html where they say

Here it's the negative charges in the wire that are moving to the left. Because they're moving, the average distance between them is length-contracted by the Lorentz factor.

OK, in the picture posted by the OP the electrons are moving to the right, but this should not make any difference.

 

[Ibix]

Maybe because of the length contraction effect?

May I take it that you didn't re-read posts #2 and #4 as I recommended in the bit of my post that you didn't quote?

The point is that when no current flows, the electrons are at rest with respect to the wire, and are 0.1nm (for the sake of argument) apart in the rest frame of the wire. When the current flows, the electrons are moving. Unless electrons have appeared from nowhere they must still be 0.1nm apart in the rest frame of the wire. All that means is that they aren't 0.1nm apart in their own rest frame. But why should they be? They don't form a solid body held together by internal forces. They can be whatever distance apart they like and accelerated bodies don't necessarily end up the same distance apart in their final rest frame as they were in their original frame.

 

[Dale]

Maybe because of the length contraction effect? You can find it explained in many educational resources, for instance in http://physics.weber.edu/schroeder/mrr/MRRtalk.html where they say

Here it's the negative charges in the wire that are moving to the left. Because they're moving, the average distance between them is length-contracted by the Lorentz factor

Read the reference you cited. Nowhere does it use length contraction to claim that the wire is charged in the lab frame. It uses length contraction, plus the fact that the wire is not charged in its rest frame, to show that it is charged in other frames.

 

[Strilanc]

Let's think about train cars instead of electrons. You start with this situation:

  ...     [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    ...

  ...     [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    ...

Then you make all of the cars in the top line accelerate to a high speed simultaneously w.r.t. the initial frame. This contracts them each individually:

                      --- moving right FAST ---->
  ...      [[]      [[]      [[]      [[]      [[]      [[]      [[]      [[]      [[]      [[]      [[]     ...

                still stopped
  ...     [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    [[[[]    ...

If we then transform into the frame of the now-moving cars, we get this:

                at rest w.r.t. current frame
  ...      [[[[]           [[[[]           [[[[]           [[[[]           [[[[]           [[[[]           [[[[]  ...

                      <---- moving left FAST -------
  ...     [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  [[]  ...

The reason that the top cars are more spread out in the second frame than they were when at rest in the starting frame is that, in the second frame, they did not all start moving simultaneously. The ones further ahead accelerated earlier. The reason that the bottom cars are bunched together, instead of being contracted individually, is also because of simultaneity changes.

The same logic applies to the wire and the electrons. If the charges all start moving at the same time in the starting rest frame, then the electrons *individually* contract instead of globally contracting and bunching up. (One potential area for confusion is if you imagine a battery at one end turning on to push charge down the wire. In that case the charges won't start moving simultaneously, and there will be bunching up.)

 

[A.T.]

Maybe because of the length contraction effect?

Length contraction relates distances in different frames for the same situation, not lengths in one frame for different situations.

 

[A.T.]

Let's think about train cars instead of electrons.

That's some great ASCII art. Here is a nice diagram by DrGreg:

https://www.physicsforums.com/threads/explanation-of-em-fields-using-sr.714635/page-2#post-4528480

 

[Fantasist]

May I take it that you didn't re-read posts #2 and #4 as I recommended in the bit of my post that you didn't quote?

No, I did not read it again. I don't think these posts are appropriate responses to the OP.

 

[Fantasist]

That's some great ASCII art. Here is a nice diagram by DrGreg:

https://www.physicsforums.com/threads/explanation-of-em-fields-using-sr.714635/page-2#post-4528480

Well, you have now kind of 'outsourced' the charge conservation violation by shifting the surplus charges to a different section of the wire. The question is how do the electrons 1,2,3,6,7,8 manage to get instantaneously from the bottom section of the loop to the top section as soon as the Lorentz boost is applied. This does not seem be to be a physically realistic assumption. And anyway, it appears to contradict the theory: from the bottom section of the loop (current flowing), you can read off that the velocity v of the current corresponds to a relativistic factor γ(v)=4 i.e. v/c=sqrt(1-1/16). Using the velocity addition theorem I thus get for the relativistic factor for the top section of the current loop γ(v_top)= 31 , so this means according to Relativity there should be 31*2=62 blue charges in the top section not 14 as shown. But this would obviously violate charge conservation.

 

[Strilanc]

If we're talking about a loop, instead of infinitely long wires, then presumably it works like the spokes on a wheel.

http://casa.colorado.edu/~ajsh/sr/wheel.html:

http://casa.colorado.edu/~ajsh/sr/contraction.html:

(Notice that it satisfies conservation-of-spokes.)

 

[Ibix]

The question is how do the electrons 1,2,3,6,7,8 manage to get instantaneously from the bottom section of the loop to the top section as soon as the Lorentz boost is applied.

Because a Lorentz boost is not a physical process, it's just a change of coordinates. It's just like scrolling a map - you aren't moving buildings, you're just drawing a different map. Similarly, applying a boost isn't accelerating, it's just drawing a map of space-time from the perspective of a moving observer. Instantaneous (or not) doesn't come into it.

 

[Ibix]

No, I did not read it again. I don't think these posts are appropriate responses to the OP.

They are (hints to) a complete answer to the OP's question.

 

[DrGreg]

you can read off that the velocity v of the current corresponds to a relativistic factor γ(v)=4

Wherever there is an arrow labelled "Lorentz contraction" in the diagram there is a factor of \gamma_1 = 2 . I don't know where you got 4 from. The single arrow labelled "more Lorentz contraction" is a "double" contraction, with a factor of \gamma_2 = 2 \gamma_1{}^2 - 1 = 7.

The question is how do the electrons 1,2,3,6,7,8 manage to get instantaneously from the bottom section of the loop to the top section as soon as the Lorentz boost is applied.

That's due to relativity of simultaneity; the boost redefines what is "simultaneous".

 

[Fantasist]

Wherever there is an arrow labelled "Lorentz contraction" in the diagram there is a factor of \gamma_1 = 2 . I don't know where you got 4 from

8/2=4

The single arrow labelled "more Lorentz contraction" is a "double" contraction, with a factor of \gamma_2 = 2 \gamma_1{}^2 - 1 = 7.

Yes, 7 is what follows from the drawing for the second contraction (14/2) , but it should be 31 if you apply the equations of relativity

 

[DrGreg]

8/2=4

The eight electrons on the left are in a wire segment that is double the length of the contracted wire segment on the right that has two electrons.

Try measuring the distances between the electrons; the ratio is 1:2 not 1:4.

(NOTE: the length contraction is between the left and right diagrams as shown by the arrows. Comparing the top diagram with the bottom is not length contraction.)

 

[Fantasist]

The eight electrons on the left are in a wire segment that is double the length of the contracted wire segment on the right that has two electrons.

Try measuring the distances between the electrons; the ratio is 1:2 not 1:4.

I was referring to the 8 red charges and 2 blue charges in the segment in the bottom right corner. I make this a charge density ratio 1/4 electrons/ions.

 

[DrGreg]

I was referring to the 8 red charges and 2 blue charges in the segment in the bottom right corner. I make this a charge density ratio 1/4 electrons/ions.

Yes it is. But I thought you were talking about length contraction between two frames of reference, not charge density ratio within a single frame.

 

[A.T.]

If we're talking about a loop, instead of infinitely long wires, then presumably it works like the spokes on a wheel.

http://casa.colorado.edu/%7Eajsh/sr/wheel.html:

http://casa.colorado.edu/%7Eajsh/sr/contraction.html:

(Notice that it satisfies conservation-of-spokes.)

It's similar but not quite the same:
- The proper distance between the spokes doesn't change between rolling and not rolling.
- The proper distance between the electrons does change between current and no current.

ETA : The above is not correct as pervect noted. The proper distance between the spokes does change.

 

[A.T.]

Yes it is. But I thought you were talking about length contraction between two frames of reference, not charge density ratio within a single frame.

That's what I tried to clarify in post #22: Using the term "contraction" for different things leads to the most confusion here.

 

[pervect]

It's similar but not quite the same:
- The proper distance between the spokes doesn't change between rolling and not rolling.
- The proper distance between the electrons does change between current and no current.

If the circumference changes, and the number of spokes around the circumference doesn't change, how can you think that the proper distance between the spokes stays constant?

 

[A.T.]

If the circumference changes, and the number of spokes around the circumference doesn't change, how can you think that the proper distance between the spokes stays constant?

You are right. The proper spoke distance changes, so it is very similar to the current loop.

 

[Histspec]

That's what I tried to clarify in post #22: Using the term "contraction" for different things leads to the most confusion here.

In the following page, length contraction in terms of measurements in different frames is called "passive", and length contraction in terms of measurements in one inertial frame is called "active"
http://www.mathpages.com/home/kmath699/kmath699.htm
It seems to me that many misunderstandings concerning the "wire-current" scenario, Bell's spaceship paradox etc. can easily be avoided by using such a terminology.

 

[DrGreg]

In the following page, length contraction in terms of measurements in different frames is called "passive", and length contraction in terms of measurements in one inertial frame is called "active"
http://www.mathpages.com/home/kmath699/kmath699.htm
It seems to me that many misunderstandings concerning the "wire-current" scenario, Bell's spaceship paradox etc. can easily be avoided by using such a terminology.

Indeed. In my diagram of post #25, "Lorentz contraction" means "passive Lorentz contraction", between left & right diagrams. There is no "active Lorentz contraction", for the electrons between top & bottom diagrams, because the electrons are not rigidly separated from each other i.e. there's nothing forcing their separation, in their own rest frame, to remain constant.

 

[DarioC]

This reminds me of a discussion we had here some time ago about current flow in a wire. I actually sat down and computed the "free" electrons in a one millimeter square wire in the first atom wide right angle sheet at the beginning of the wire. Made the wire one meter long. The number was amazingly large to me. For a guy who worked as an electronics technician all his life it shed and entirely new light on my thought process concerning current flow.

Anyway the calculations, using a current of one ampere, which is quite a bit of current for this wire, indicate that it would take a really long time for a given electron to get to the other end of the wire. I had proposed that the wire was like a long pipe full of ping-pong balls, except that the pipe is huge and the number of balls is equally huge.

That is to say you push some balls in one end and they produce and interaction between balls all the way down the wire and pop some balls out the other end.

The analogy gets really interesting when you put in a very short pulse. In the real wire the interaction must travel down the wire at close to the speed of light but the electrons don't really have to move at a very fast average speed, especially when compared to the random thermal motion, which I understand to be much larger.

I believe the number I came up with for a given electron to travel down the one meter wire, at one ampere, could be as much as 23 hours. It sounds pretty insane and I have never seen anything in print that even mentioned such a calculation. One just has to compare the number of electrons supplied by one ampere with the available number of electrons in each atom-wide sheet of a meter long wire (and how many "sheets" there are) to see that the calculation might be reasonable.

DC

 

[Orodruin]

That is to say you push some balls in one end and they produce and interaction between balls all the way down the wire and pop some balls out the other end.

This is not a good analogy. Electric current works mainly by the application of an external electric field, not through the electrons pushing each other (electrons pushing each other makes sure the conductor is electrically neutral).

One just has to compare the number of electrons supplied by one ampere with the available number of electrons in each atom-wide sheet of a meter long wire (and how many "sheets" there are) to see that the calculation might be reasonable.

All electrons are not available for conduction so the actual average electron velocity is going to be larger than what is given by this assumption.

 

[DarioC]

You might want to look at what it is that generates that electric field, say in the example of an electric cell (battery), before you disagree that the electrons are pushing against each other. Obviously the charge of each electron is what does the pushing against the charge of the other electrons, I figured everyone here would know that.

I, of course, left out a few things, like that I am talking about the number of conduction band electrons available in a copper wire, not the total quantity of electrons possessed by all the atoms.

I guess that the way I put it did leave it open for that interpretation, if you make the assumption that I am ignorant enough to think that all the electrons in an atom are involved in electrical current flow.

My point is that there is a massive amount of conduction electrons in even a small wire compared to the number of electrons supplied by what would be considered a typical flow of current in an "everyday" situation.

DC