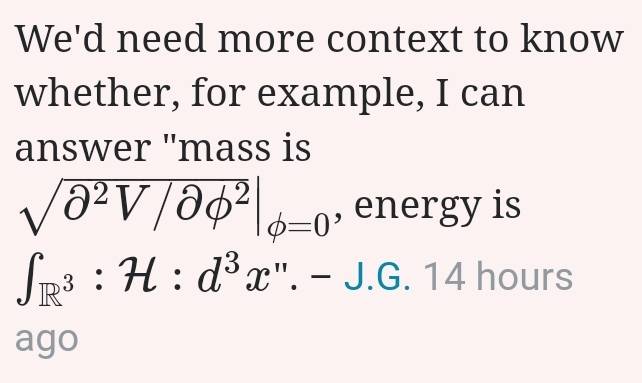Thelamon said:
inertial mass, gravitational mass, rest mass, effective mass etc. is all the same: just mass, right?
No.
According to GR, inertial mass and gravitational mass are the same, where here "gravitational mass" means what in more precise terminology would be called "passive" gravitational mass. Basically, this property determines how an object's trajectory in spacetime depends on its initial velocity and any forces it is subjected to. (Note that in GR gravity itself is not a force, and an object moving solely "due to gravity" is in free fall and feels no force, and has zero proper acceleration.)
Rest mass is the invariant length of an object's 4-momentum vector. It is conceptually distinct from inertial/gravitational mass, although in many scenarios they are numerically equivalent.
I'm not sure what you mean by "effective mass".
Thelamon said:
(And historically there was also transversal mass and longitudinal mass, electromagnetic mass, relativistic mass which is still used sometimes though. Those are things of the past so I'm not sure why I mention it).
Your hesitation is well founded. None of those concepts are useful in our best current models in physics.
Thelamon said:
And in GR there Komar mass and ADM mass.
Yes, which are both different from the above concepts, and different from each other. The most important difference between these concepts and the ones above is that Komar mass and ADM mass (and Bondi mass, which is different again) are global concepts, not local concepts, and are only valid in particular types of spacetimes.
Thelamon said:
all kinds of mass-terms or concepts of mass, which all have the same property that it has the resistance to a chance in velocity
No, they are not. See above.
Thelamon said:
I'm not sure why you say that, since previously you said the energy of a system was the same as its inertial mass.
Thelamon said:
I don't know if because E=mc^2
##E = mc^2## is actually not a very useful equation. It can be viewed either as a simple tautology describing a conversion of units--i.e., a given quantity in energy units is the same as that quantity in mass units multiplied by the speed of light squared--or as a special case of the relativistic energy-momentum relation ##E^2 - p^2 c^2 = m^2 c^4##, where ##m## is the rest mass (or invariant mass, which is a better term).
Thelamon said:
QM deals with the concept of energy the same as with (inertial) mass?
in QM in general, "energy" is an observable (mathematically it is described by an operator, the Hamiltonian). This observable would tell you the inertial properties of the system you are observing, so it could be taken as also telling you a system's inertial mass, but cases in QM in which that is relevant are rare.
In QFT, the term "mass" is usually used to describe an inherent property of particles (or more precisely quantum fields). In this usage it more or less corresponds with the classical concept of rest mass/invariant mass.