ValeForce46
- 40
- 3
- Homework Statement
- A tube of mass ##M= 18 kg ##, section ##A= 300 cm^2 ## and lenght ##l= 200 cm ## is sealed to the top and opened to the bottom. Initially the tube contains only air at a pressure ##p_0= 1 bar ##, occupying the whole volume ##A*l ## (see picture a). Then, the tube is leaning on a surface of alcol (density ##ρ=0.8 g/cm3 ##) and, keeping the tube vertically, it is immersed until it reaches a position of balance. In this process the air inside the tube is compressed (see picture b).
In conditions of equilibrium, calculate:
a)the pressure ##p ## of the air inside the tube;
b)the difference of level ##d ## between the surface of the alcol inside and outside the tube;
c)the length ##b ## of the tube which emerges.
- Relevant Equations
- Stevino's Law ##p=p_0+ρ*g*h ##
Force caused by pressure ##F=p*A##
This is a problem from a past exam.
For point a)
the balance between force should be given by the following equation
$$M*g+p_0*A=ρ*g*(A*d)+p*A$$
But I still have two unknown values...
I know that pressure outside the tube at depth d is
$$p(d)=p_0+ρ*g*d$$
and this has to be equal to the pressure at depth d inside the tube, because that's a free surface.
What do I do now? Is the equation of the balance of the forces correct?
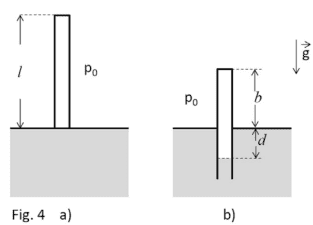
For point a)
the balance between force should be given by the following equation
$$M*g+p_0*A=ρ*g*(A*d)+p*A$$
But I still have two unknown values...
I know that pressure outside the tube at depth d is
$$p(d)=p_0+ρ*g*d$$
and this has to be equal to the pressure at depth d inside the tube, because that's a free surface.
What do I do now? Is the equation of the balance of the forces correct?
 !
!
