I Is the Blade Loading Sufficient for Minimum Sliding Resistance at Top Speed?

AI Thread Summary
The discussion revolves around assessing whether the blade loading of a model, designed to measure air resistance on ice, is sufficient to minimize sliding resistance at high speeds. The model features three stainless steel blades, each 30 cm long and 1 mm thick, with a top speed of 90 kph and a calculated loading of 0.67 kg/cm². The user is considering adjusting the weight or blade lengths to optimize performance. They acknowledge the importance of pressure between the blades and the ice, as well as the impact of ice temperature. The user plans to enhance the model by adding pressure sensors to each blade for more accurate readings.
Colin Wilson
Messages
7
Reaction score
4
I'm building a model as shown below (side, front, back). In order to measure its air resistance I will be mounting it on temporary ice blades (Green) and driving it down a long skating rink. The model has a pressure sensor incorporated into the motor / propeller assembly and a GPS unit to measure velocity, a microcontroller collects the data (pressure / velocity) and writes it to an SD card. As it sits the blade loading would be as follows:
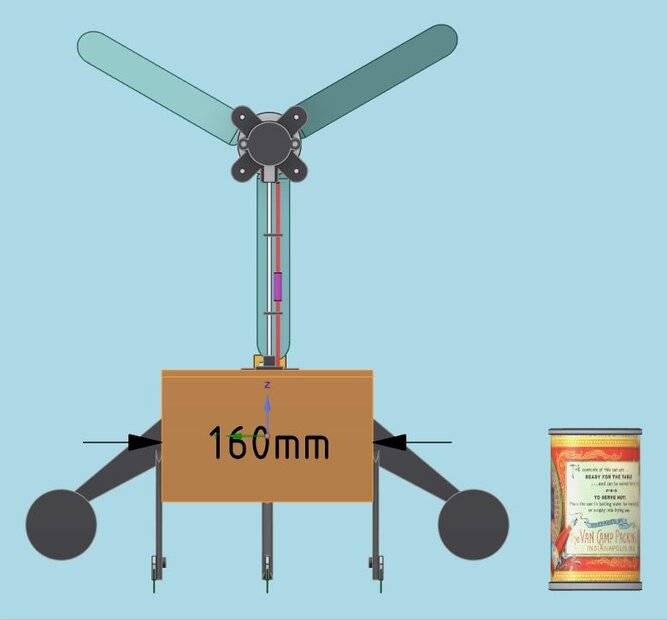
  • (3) SS blades = 30cm long * 1mm thick
  • Top speed 90kph (82fps)
  • Loading 2kg per blade = 0.67kg / cm2
My question: Is the blade loading high enough given the top speed to ensure minimum sliding resistance? I can add more weight to the model or I can reduce the blade lengths.
DB Slim Test Sled Side.jpg
DB Slim Body Front.jpg
DB Slim Test Sled Back.jpg
 
Physics news on Phys.org
I searched ice skate friction, and found myself traveling down a rabbit hole of interesting information. But I did not find an answer to your question. You apparently already understand that pressure between the skate blades and the ice is a key variable, as is also the ice temperature.

I suggest that you treat the blade loading as an experimental variable, and run a series of experiments to optimize it.
 
Reply
  • Like
Likes Colin Wilson
Thank you for your input.
In any case woke up this morning and decided to put pressure sensors on each blade and subtract those readings from the motor reading so problem solved!
 

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

4 hard (long) problems- problem set.
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top