Is the Book's Answer Correct for This Circuit Problem?

[KingNothing]

Hey everyone, this is a problem straight from my book. It's an odd number, so the book has the answer in the back: 4.7 ohms

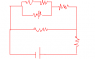
The setup is near impossible to explain, so I've attached a diagram of the setup. Basically, it is a circuit with some resistors (represented by squiggly lines) each with R=2.8 kilo-ohms.

I came up with:
R=(\frac{1}{3*2.8}+\frac{1}{2*2.8}+\frac{1}{2.8})^-1+2.8=4.33\Omega
The -1 right after the frist parentheses is a ^-1, it's kind of hard to tell.
Did I do it wrong? Is the book wrong? Is it just a case where they rounded and I didnt?

 

[gnome]

Are you sure the diagram you posted is correct? Your equation has 7 resistors but I see only 6 in the diagram.

 

[KingNothing]

Yes, I'm fully aware of that...you see, I figured that if it exits the smaller line there on the bottom, and travels up to the intersection, that if it took either of the two uppermost paths (speaking literally according to diagram) that it would have to pass through the upper resistor on the right side, so I accounted for that twice. What is the proper way to do this?

 

[enigma]

The two in the top left are in series, and are in parallel with the diagonal. That grouping is in series with the top one on the right. That whole grouping is in parallel with the middle one. Then that whole thing is in series with the bottom one on the right.

 

[gnome]

It certainly doesn't go through any resistor twice.

First I'd re-draw the diagram to make it less confusing. Then I think the solution is pretty easy. But I don't get your book's answer either. I get 4.55 \Omega

 

[ShawnD]

I get 4.55

I broke it into 3 parts.
1. solve for 4 top resistors (as a parallel circuit)
2. solve for the middle resistor in parallel with the top 4
3. add the 1 resistor in series

Here is what the top 4 resistors are like, I think.

2.8 + [2.8^{-1} + [(2)(2.8)]^{-1}]^{-1}

Now write that as A in your calculator. Trying to sub that into an even more complicated equation will just cause problems.

Now here is what the parallel portion of the entire circuit looks like

[2.8^{-1} + A^{-1}]^{-1}

Now add the series portion which is just 2.8

R = 2.8 + [2.8^{-1} + A^{-1}]^{-1}

R = 4.55

 

[KingNothing]

Thank you everyone...I can't tell you how relieving it is to see exactly what I did wrong. It's such a great feeling! Thank you a ton Shawn and enigma and gnome. I got 4.55 as well.