Saw
Gold Member
- 631
- 18
This is a recapitulation of a subject that has incidentally appeared in another thread (Light shone in a train bouncing off mirrors…) that started over another issue (why does light take the direction of the source but not its speed?), although there may be a connection between the two things.
I have already received some helpful comments, but I still have doubts. If you find this introduction too long, please jump to the next post, which is where I place the question that worries me now.
The subject is to judge if the duel described by Brian Greene in the Fabric of Cosmos (when explaining the relativity of simultaneity) is “fair”, in its original version and with a variation.
JesseM confirmed that the answers to questions (a) and (c) is:
And to question (b):
We still discussed for a while whether the question “is the duel fair?” is purely legal or also physical, but I think in the end we agreed that:
- The legal problem is the same as the physical problem. The role of the law is to solve problems, just as the role of physics is to solve problems.
- The legal problem is not to establish some arbitrary conventional rules for the game. The rules, on top of being agreed upon, must ensure that both duellers have “equal opportunities” to shoot and avoid being shot. For example, after receiving the signal for shooting and before being shot, the duellers may stand aside, duck down or try any other tricks. Do they dispose of the same time for this purpose?
- This legal need can be translated into a well-defined physical expression:
(I initially contested the definition, but I was wrong. In the end I agree that it was perfectly appropriate.)
In other words, the law requires that the duellers can do equal number of “tricks” to win. Physics answers that that means that their clocks register the same number of “ticks”, but in particular SR specifies that the relevant ticks are “proper” ticks, those of the duellers or of assistants situated where they receive the signals and the shots.
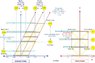
These are the calculations assuming that the relative velocity of the train wrt the ground is 0.5 c and that the train is 2 ls long in its rest frame (1.732 ls in the ground frame):
- In the train frame: Back and Front get the light signals simultaneously (after 1s) and their shots take 2 s to reach their opponents. So the proper time interval is 2s for both duellers. The duel is fair.
- In the ground frame, the duel is also fair because the proper time interval, although another one, is also the same for both duellers:
* Back got the light signal earlier (0.577 s) because he was heading towards the signal (thus making its path shorter), which looks like an advantage, but then it also happens that he is shot earlier (2.886 s), for the same reason, because he was heading towards the laser (thus making its path shorter), which is a disadvantage. The interval is 2.886 - 0.577 = 2.309 s.
* Front got the light signal later (1.732 s) because she was racing away from the light (thus making its path longer), which looks like a disadvantage, but then it also happens that he receives the shot earlier (3.732 s), for the same reason, because she was escaping from the bullet (thus making its path longer). The interval is 3.732 – 1.732 = 2.309 s.
Then we engaged in a challenging discussion about what it means that, as observed in the ground frame, the duellers get the light signals non-simultaneously.
My final understanding, as referee in the ground, is very prudent: the physical fact about it is that, if the clocks of my assistants (situated by Back and Front when they received the light signals) had been synchronized following the Einstein convention, they would show different readings; but this is just a piece of the puzzle; if I want to rule, I have to compare the clock readings at reception of the light signal with the clock readings of other assistants witnessing the reception of the shots; the latter are also non-simultaneous; the difference is the same for both duellers = they disposed of the same proper ticks to do their proper tricks.
Thus I rule, in accordance with the advice of SR experts, that the duel was fair.
Now we face a variation of the same duel: the signals for shooting are still light signals but the duellers shoot mechanical bullets.
What I have studied about SR tells me that the solution must be identical, since mechanical objects obey the same laws of physics:
- In the train frame: just like the light signals travel equal paths at the same speed (c) and arrive simultaneously at the duellers, their bullets also travel the same paths at the same speed and hit simultaneously the duellers.
- In the ground frame, you can reach the same conclusion through two routes:
* If I apply the relativistic formula for the addition of velocities to the light signals, I will discover that they still travel wrt me at c. And if I apply it to the bullets, I will find a differential element. Each bullet travels at a different speed wrt me, but this fact does not change the judgment: the bullet from Back travels wrt me faster than the bullet from Front, but less fast than it would if we had applied the Galilean addition formula (which compensates for the fact that it departs earlier) and the bullet from Front travels less slowly than it would with the Galilean formula (which compensates for the fact that it departs later).
* If, with the aid of my assistants, I measure directly the speed of the light signals and the bullets, I will find that they travel at exactly the speeds that stem from the above formulas.
However, I have doubts: due to some reasoning about the difference between what is “real” and “conceptual” (which I will not repeat here, it’s just too long), I fear that, in this new case, the proper time intervals (during which the duellers must do their tricks) should be different. I don’t know who would have the advantage and, in any case, the difference would be tiny. But this would make the duel, by definition, unfair, in the opinion of both referees.
Nevertheless, I conclude: if the experts tell me that the solution to the thought experiment I describe in the next post is “yes” (and maybe you give some sort of explanation for that, it doesn’t have to be very profound, I want to finish my job!), I will rule as proposed by SR.
Please give me a hand!
I have already received some helpful comments, but I still have doubts. If you find this introduction too long, please jump to the next post, which is where I place the question that worries me now.
The subject is to judge if the duel described by Brian Greene in the Fabric of Cosmos (when explaining the relativity of simultaneity) is “fair”, in its original version and with a variation.
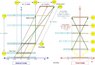
Saw said:There is a duel on a train, between duellers that we will call Back and Front, situated at the tail and the tip of the car, respectively. For their duel, they employ laser guns, of identical construction.
There are two referees: Althonhare, on the train, and myself, Saw, on the ground. The signal for the commencement of the duel is given at the precise instant when Althon and myself are lined up. Of course, it is impossible that the two referees occupy the same position in space and so the perception of this alignment would require light traveling some distance from one to the other. But we stipulate that the distance is so small that its consequences are negligible. We all agree that the alignment (which is a single event) is simultaneous in both frames.
In order to give the duellers the signal for shooting, a pile of gunpowder, set midway between them (i.e., where Althon, on the car, and myself, on the ground, are standing at that instant), explodes and thus sends flashes of light in both directions.
Was the duel fair?
Each referee has a different opinion:
* Althon is certain that light from the flare reaches the duelers simultaneously, so he raises the green flag and declares it a fair draw.
[More technically: In the train frame, the light pulses travel equal paths in their respective directions and do it at the same speed. So the two distant events (= arrival of the signals to shoot) are SIMULTANEOUS.)
* According to the author, I wildly squeal foul play, claiming that Back got the light signal from the explosion before Front did. I explain that, because the train was moving forward, Back was heading toward the light while Front was moving away from it. This means that the light did not have to travel quite as far to reach Back, since he moved closer to it; moreover, the light had to travel farther to reach Front, since he moved away from it. Since the speed of light, moving left or right from anyone’s perspective, is constant, I am supposed to claim that it took the light longer to reach Front, since it had to travel farther, rendering the duel unfair.
[Idem: In the ground frame, light towards Back travels a shorter path, since its target is heading towards it, while light towards Front travels a longer path, since its target is escaping away. As both pulses travel at the same speed, the one that hits Back arrives earlier than the one that hits Front. The two distant events are NOT SIMULTANEOUS.]
Who is right? The matter is not trivial, because the judge who has made a mistake will be sanctioned by the competent supervision body and he may not be able to exercise his profession any more.
Fortunately (?), Einstein comes to the rescue of both with a salomonic opinion:
“Einstein’s unexpected answer is that they both are (…) they simply have different perspectives on the same sequence of events. The shocking thing that Einstein revealed is that their different perspectives yield different but equally valid claims of what events happen at the same time. Of course, at everyday speeds like that of the train, the disparity is small – Saw claims that Front got the light less than a trillionth of a second after Back- but were the train moving faster, near light speed, the time difference would be substantial” (literal quotation, I just changed the names).
But I am a prudent referee. I try to do my job properly. I know that the words of the law (you shall raise a green flag if the duel is “fair”) have a practical purpose and I must interpret them in the light of this practical purpose. The duel is “fair” if the two duellers are given equal opportunities of hitting each other, in practical terms. So my opinion that “Back got the signal earlier” is only relevant for the matter to be judged if it gives Back a real advantage (or disadvantage!).
To this effect, I consider the following scenarios:
(a) Back sees the signal earlier and fires earlier as well. Can his laser pulse hit Front before the latter receives the signal?
(b) If not, they have both received the signals and shot their laser pulses. The latter will also take some time to reach their targets. During this time interval, theoretically, any dueler could try the usual trick: fire and stand aside, before being wounded. There is very little time for this deed, especially if we talk about laser guns, but we can imagine the distance arbitrary long for this purpose. Is this time interval longer for Back than for Front or vice versa?
(c) If not, we imagine Back badly wounded, kneeling on the floor of the car, but brave enough to fire a second shot. Can it reach Front before the latter has the opportunity to fire his own second shot…?
You can think of other scenarios if you wish. The more, the better. That is the point of the exercise.
Then I call a group of experts on SR and ask their answers to the practical questions. If the answers, as I expect, are negative (there is no breach of the principle of equal opportunities), then I do not “wildly squeal foul play” as Brian Greene suggests. Instead, I gently and gallantly raise a green flag, in agreement with Althonhare’s opinion.
JesseM confirmed that the answers to questions (a) and (c) is:
JesseM said:No. If two events are simultaneous in any frame, that must mean there is a spacelike separation between the two events, meaning neither event lies in the other event's future light cone.
And to question (b):
JesseM said:Same time for both, since they're both at rest in the train frame, and they both fire at the same moment in this frame.
We still discussed for a while whether the question “is the duel fair?” is purely legal or also physical, but I think in the end we agreed that:
- The legal problem is the same as the physical problem. The role of the law is to solve problems, just as the role of physics is to solve problems.
- The legal problem is not to establish some arbitrary conventional rules for the game. The rules, on top of being agreed upon, must ensure that both duellers have “equal opportunities” to shoot and avoid being shot. For example, after receiving the signal for shooting and before being shot, the duellers may stand aside, duck down or try any other tricks. Do they dispose of the same time for this purpose?
- This legal need can be translated into a well-defined physical expression:
.JesseM said:"the duel is fair if each dueller experiences the same proper time between firing their own gun and the laser from the other guy's gun reaching their position"
(I initially contested the definition, but I was wrong. In the end I agree that it was perfectly appropriate.)
In other words, the law requires that the duellers can do equal number of “tricks” to win. Physics answers that that means that their clocks register the same number of “ticks”, but in particular SR specifies that the relevant ticks are “proper” ticks, those of the duellers or of assistants situated where they receive the signals and the shots.
These are the calculations assuming that the relative velocity of the train wrt the ground is 0.5 c and that the train is 2 ls long in its rest frame (1.732 ls in the ground frame):
- In the train frame: Back and Front get the light signals simultaneously (after 1s) and their shots take 2 s to reach their opponents. So the proper time interval is 2s for both duellers. The duel is fair.
- In the ground frame, the duel is also fair because the proper time interval, although another one, is also the same for both duellers:
* Back got the light signal earlier (0.577 s) because he was heading towards the signal (thus making its path shorter), which looks like an advantage, but then it also happens that he is shot earlier (2.886 s), for the same reason, because he was heading towards the laser (thus making its path shorter), which is a disadvantage. The interval is 2.886 - 0.577 = 2.309 s.
* Front got the light signal later (1.732 s) because she was racing away from the light (thus making its path longer), which looks like a disadvantage, but then it also happens that he receives the shot earlier (3.732 s), for the same reason, because she was escaping from the bullet (thus making its path longer). The interval is 3.732 – 1.732 = 2.309 s.
Then we engaged in a challenging discussion about what it means that, as observed in the ground frame, the duellers get the light signals non-simultaneously.
My final understanding, as referee in the ground, is very prudent: the physical fact about it is that, if the clocks of my assistants (situated by Back and Front when they received the light signals) had been synchronized following the Einstein convention, they would show different readings; but this is just a piece of the puzzle; if I want to rule, I have to compare the clock readings at reception of the light signal with the clock readings of other assistants witnessing the reception of the shots; the latter are also non-simultaneous; the difference is the same for both duellers = they disposed of the same proper ticks to do their proper tricks.
Thus I rule, in accordance with the advice of SR experts, that the duel was fair.
Now we face a variation of the same duel: the signals for shooting are still light signals but the duellers shoot mechanical bullets.
What I have studied about SR tells me that the solution must be identical, since mechanical objects obey the same laws of physics:
- In the train frame: just like the light signals travel equal paths at the same speed (c) and arrive simultaneously at the duellers, their bullets also travel the same paths at the same speed and hit simultaneously the duellers.
- In the ground frame, you can reach the same conclusion through two routes:
* If I apply the relativistic formula for the addition of velocities to the light signals, I will discover that they still travel wrt me at c. And if I apply it to the bullets, I will find a differential element. Each bullet travels at a different speed wrt me, but this fact does not change the judgment: the bullet from Back travels wrt me faster than the bullet from Front, but less fast than it would if we had applied the Galilean addition formula (which compensates for the fact that it departs earlier) and the bullet from Front travels less slowly than it would with the Galilean formula (which compensates for the fact that it departs later).
* If, with the aid of my assistants, I measure directly the speed of the light signals and the bullets, I will find that they travel at exactly the speeds that stem from the above formulas.
However, I have doubts: due to some reasoning about the difference between what is “real” and “conceptual” (which I will not repeat here, it’s just too long), I fear that, in this new case, the proper time intervals (during which the duellers must do their tricks) should be different. I don’t know who would have the advantage and, in any case, the difference would be tiny. But this would make the duel, by definition, unfair, in the opinion of both referees.
Nevertheless, I conclude: if the experts tell me that the solution to the thought experiment I describe in the next post is “yes” (and maybe you give some sort of explanation for that, it doesn’t have to be very profound, I want to finish my job!), I will rule as proposed by SR.
Please give me a hand!
Last edited: