- #1
Saw
Gold Member
- 631
- 18
A FAQ is why the spacetime interval has a minus sign.
A geometrical answer is that the interval is always the shortest path (the straight line) between two points. If we talk about spatial points, that interval is the hypotenuse of a right angle triangle, whose sides are the projections of such path over the X and Y axes of any coordinate system, no matter its orientation (that is, after rotation). If we talk instead about spacetime points (events), the shortest path turns out to be, instead, the height of the triangle, formed in this case by the projections over the Time (hypotenuse) and the X (basis) axes.
One does not visualize that, however, in a Minkowski diagrams, where you either have:
(i) two independent drawings (one for each frame) or
(ii) two overlapping drawings, where one has perpendicular axes, whilst the other's are rotated in opposite directions.
I have looked for an alternative. Epstein diagrams (see the book "Relativity visualized") are interesting, because he plays with proper time, which is after all what goes in 4-velocity, but they are single diagrams. A step further was this picture, based on which I have drawn this other one:
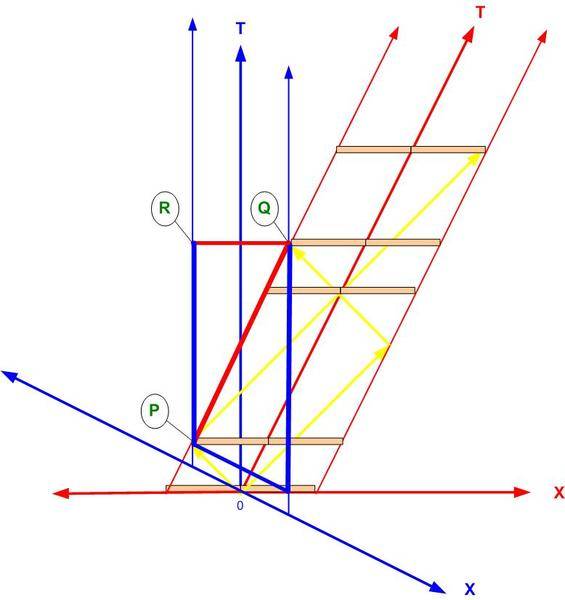
A little explanation:
v = 0.5 c
The thick blue line connecting (timelike) events P and R is the proper time and the height of the triangle whose hypotenuse is the red coordinate time and whose basis is the red coordinate length separating those events.
The thick red line connecting (timelike) events P and Q is the proper time and also the height of the triangle whose hypotenuse is the blue coordinate time and whose basis is the blue coordinate length between those events.
Interesting, isn´t it? Any comment?
A geometrical answer is that the interval is always the shortest path (the straight line) between two points. If we talk about spatial points, that interval is the hypotenuse of a right angle triangle, whose sides are the projections of such path over the X and Y axes of any coordinate system, no matter its orientation (that is, after rotation). If we talk instead about spacetime points (events), the shortest path turns out to be, instead, the height of the triangle, formed in this case by the projections over the Time (hypotenuse) and the X (basis) axes.
One does not visualize that, however, in a Minkowski diagrams, where you either have:
(i) two independent drawings (one for each frame) or
(ii) two overlapping drawings, where one has perpendicular axes, whilst the other's are rotated in opposite directions.
I have looked for an alternative. Epstein diagrams (see the book "Relativity visualized") are interesting, because he plays with proper time, which is after all what goes in 4-velocity, but they are single diagrams. A step further was this picture, based on which I have drawn this other one:
A little explanation:
v = 0.5 c
The thick blue line connecting (timelike) events P and R is the proper time and the height of the triangle whose hypotenuse is the red coordinate time and whose basis is the red coordinate length separating those events.
The thick red line connecting (timelike) events P and Q is the proper time and also the height of the triangle whose hypotenuse is the blue coordinate time and whose basis is the blue coordinate length between those events.
Interesting, isn´t it? Any comment?
Last edited: