Is there a conflict between CPT symmetry and the 2nd law of thermodynamics?

[Jarek 31]

Naively there is a conflict between CPT symmetry being at heart of fundamental physics models like QFT, and 2nd law of thermodynamics: saying that entropy grows toward future.
Is there really a conflict here - so is physics symmetric or not? How to understand it?

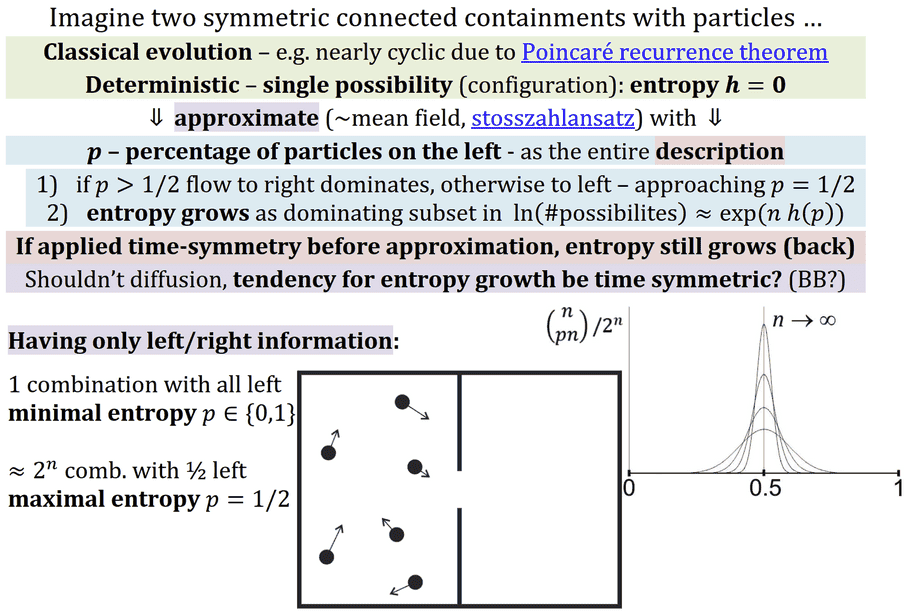
Personally I disagree with that there is conflict: to "prove" entropy growth e.g. in Boltzmann H-thoerem, we need to make this "stosszahlansatz" assumption, which corresponds to kind of mean-field approximation, allowing to prove entropy growth.
Without this approximation/smoothing, we have e.g. positions of particles with time/CPT symmetric behavior: if "proving" entropy growth, we could perform symmetry first and apply this proof - getting contradiction.

So this tendency for entropy growth seems in fact time symmetric: having low entropy situation (e.g. all particles are in left hand side of a containment), the entropy should grow if evolving toward both future and past.
Low entropy situation in the history of our Universe was our Big Bang - can BB be seen as the reason of entropy growth we are observing?

Yesterday PBS " The Arrow of Time and How to Reverse It":

 

[Tertius]

This is still an open question.
Yes, CPT symmetry suggests that all fundamental processes are reversible. We have no experimental evidence to the contrary.
Yes, all evidence of macroscopic systems, i.e. large configurations of particles undergoing physical processes shows that they are irreversible processes.

The basic theories are based on symmetry (general relativity and QFT) so they don't have any built in entropy. General relativity is time symmetric, as is QFT.

In my view, we see macroscopic events as irreversible because of how much space there is. For example, if you watch a muon decay into an electron and two neutrinos, you will have one particle become 3. In the Feynman diagram, you can just as easily combine the two neutrinos and electron back into the muon. It is reversible. So, why doesn't it ever happen? Space is big compared to the fundamental processes, and the odds of the particles aligning just right to recombine back into the muon are very low. Get rid of the enormity of space, and things will happen reversibly just fine. Technically, what happens is when you calculate the cross section for the interaction of two neutrinos and an electron, it is just way too small to ever happen. However, the decay time for a muon is only a few microseconds, so it'll happen all day!