Mathematech said:
[...] Because V and hence the Lagrangian are only defined up to the addition of an arbitrary constant, its the changes in value that matter not the actual value.
Let me elaborate on that aspect of
changes in value.
I take the following case: an object is thrown upward. Gravity decelerates it, the object reaches its highest point, gravity accelerates it on the way back down.
The work/energy theorem expresses that at each point in time the
rate of change of kinetic energy matches the
rate of change of potential energy. The two change in opposite directions, but they are at all points in time a match for each other.
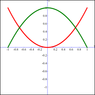
The graph of the kinetic energy as a function of time (red line) is a parabola. The graph of the potential energy as a function of time (green line) is a parabola too.
Mirror the graph of the potential energy with respect to the horizontal axis, so that it is upside down. Now the two parabola's are pointing in the same direction. For the true trajectory you have the following property: the two graphs are parallel at each point in time.
We have the common Lagrangian:
L = T - V
The minus sign corresponds to the graph of the potential energy being turned upside down.
The boundary of the shaded region represents the sum of the red graph and the green graph. As we know the Action is the integral of the Lagrangian from the start point to the end point. So the surface area of the shaded region corresponds to the Action of the Principle of Least Action.
As we know, to find the true trajectory you try a range of possible trajectories, and you find the magnitude of the Action as a function of some parameter that sweeps out the range of possible trajectories.
The Action is least when at every point in time the rate of change of kinetic energy matches the rate of change of potential energy.