patric44
- 308
- 40
Homework Statement:: i saw this simple derivation of the uncertainty principle in my college introductory quantum book
Relevant Equations:: Δp.Δx = h
hi guys
i saw this derivation of the uncertainty principle in my college quantum book , but the derivation seems very simple and sloppy , i mean the i saw multiple derivations of the uncertainty principle using Fourier analysis and Schwarz inequality and so on , so this derivation seems so simple to be true ?!
the derivation goes like this :
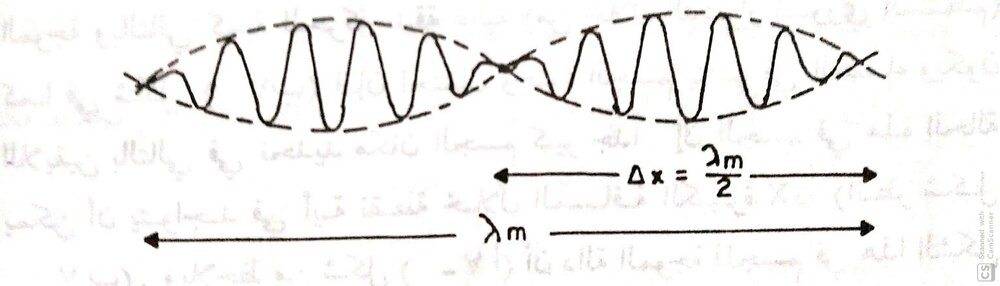
assume that the wave function of the particle is given by this figure , then the uncertainty of the position
$$Δx = \frac{λ_{m}}{2}$$
this can be written as :
$$λ_{m} = \frac{2\pi}{\frac{1}{2}Δk} ⇒$$
$$Δx = \frac{2\pi}{Δk}$$
and since
$$k = \frac{2\pi}{h}p ⇒ Δk = \frac{2\pi}{h}Δp ⇒ Δp = \frac{h}{2\pi}Δk $$
and so :
$$ΔxΔp = h$$
my objection is that the derivation seems very simple , and that the wave function itself don't describe the position of the particle as it was stated ?! so is this a valid but rather crude derivation of the uncertainty principle or its a nonsense ! and why .
Relevant Equations:: Δp.Δx = h
hi guys
i saw this derivation of the uncertainty principle in my college quantum book , but the derivation seems very simple and sloppy , i mean the i saw multiple derivations of the uncertainty principle using Fourier analysis and Schwarz inequality and so on , so this derivation seems so simple to be true ?!
the derivation goes like this :
assume that the wave function of the particle is given by this figure , then the uncertainty of the position
$$Δx = \frac{λ_{m}}{2}$$
this can be written as :
$$λ_{m} = \frac{2\pi}{\frac{1}{2}Δk} ⇒$$
$$Δx = \frac{2\pi}{Δk}$$
and since
$$k = \frac{2\pi}{h}p ⇒ Δk = \frac{2\pi}{h}Δp ⇒ Δp = \frac{h}{2\pi}Δk $$
and so :
$$ΔxΔp = h$$
my objection is that the derivation seems very simple , and that the wave function itself don't describe the position of the particle as it was stated ?! so is this a valid but rather crude derivation of the uncertainty principle or its a nonsense ! and why .