I Is this just a typo in Schutz' book on General Relativity?

Click For Summary
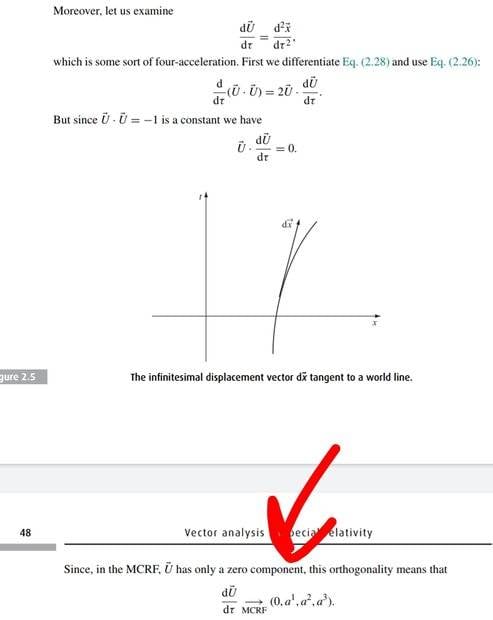
The discussion centers on a potential typo in Schutz's book regarding the four-acceleration in General Relativity. Participants clarify that the text is accurate, stating that in the momentarily comoving inertial frame, the time component of the four-acceleration is indeed zero. It is emphasized that the only non-zero component of the four-velocity is the zeroth one, leading to the correct interpretation of the four-acceleration's orthogonality to the four-velocity. However, there is a consensus that the writing lacks clarity, suggesting it would be better if Schutz had specified that the four-velocity has only a non-zero zeroth component. Overall, while the physics is sound, the need for clearer writing and better editing is noted.
Ahmed1029
Messages
109
Reaction score
40
I'm wondering is I'm missing something, or this should be " a non-zero component"?
Screenshot_2022-12-06-19-25-32-84_e2d5b3f32b79de1d45acd1fad96fbb0f.jpg
 
Physics news on Phys.org
The book is correct. In the momentarily comoving inertial frame the time component of the four-acceleration is indeed 0.
 
Reply
  • Like
Likes malawi_glenn and Ahmed1029
No, it means that in the MCRF the only non-zero component of ##\tilde{U}## is the zeroth one (because the three velocity is zero by definition in that frame). Hence the four acceleration (which he's just proved is orthogonal to ##\tilde{U}##) must take the form given.

I agree it's not particularly clearly written - it would be better if he'd said "##\tilde{U}## has only a ##{\tilde{U}}^0## component".
 
Last edited:
Reply
  • Like
Likes SiennaTheGr8, vanhees71, Dale and 1 other person
Ah yes, it's clear now. I thought he meant that it had only one component taking the value zero, which didn't make sense.
 
Reply
  • Like
Likes vanhees71 and Ibix
I must say this isn't the only thing I've found confusing in Schutz. The physics is sound enough, but I do feel like he really needed a better editor.
 
Last edited:
Reply
  • Like
Likes vanhees71 and Ahmed1029

Thread 'Physical Interpretation of Frame Field'

Moderator's note: Spin-off from another thread due to topic change. In the second link referenced, there is a claim about a physical interpretation of frame field. Consider a family of observers whose worldlines fill a region of spacetime. Each of them carries a clock and a set of mutually orthogonal rulers. Each observer points in the (timelike) direction defined by its worldline's tangent at any given event along it. What about the rulers each of them carries ? My interpretation: each...
View full post »

Similar threads

A Understanding Frame Fields in GR: A Beginner's Guide
  • · Replies 7 ·
Replies
7
Views
2K
I Taylor Expansion of Metric Transformation in RNCs
  • · Replies 9 ·
Replies
9
Views
2K
I Arguments leading to the speed of light as a dimensionless constant
  • · Replies 64 ·
3
Replies
64
Views
5K
I When time is not orthogonal to phi, that means there is a preferred direction in space? How?
  • · Replies 14 ·
Replies
14
Views
1K
I Stress-energy tensor and energy/momentum conservation clarification
  • · Replies 21 ·
Replies
21
Views
3K
I Construct a Diagram that Illustrates The Galilean Law of Addition of Velocities
  • · Replies 7 ·
Replies
7
Views
2K
I Question about Two Clocks in this Relativity scenario
  • · Replies 10 ·
Replies
10
Views
1K
I An alternative derivation of the equation of motion in General Relativity
  • · Replies 0 ·
Replies
0
Views
1K
I Radius Excess of Curvature in Relativity: Explained
  • · Replies 6 ·
Replies
6
Views
2K
I Does the metric in general relativity depend only on position because of the equivalence principle?
  • · Replies 16 ·
Replies
16
Views
2K