Discussion Overview
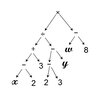
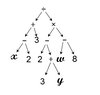
The discussion revolves around the construction and evaluation of trees representing a specific algebraic expression. Participants are examining the correctness of their trees and the results of various tree traversal methods (preorder, inorder, postorder). The focus is on the representation of the expression and the implications of operator precedence.
Discussion Character
- Exploratory, Technical explanation, Debate/contested, Mathematical reasoning
Main Points Raised
- Some participants present two trees for the same algebraic expression and express uncertainty about their correctness.
- One participant suggests that both trees could be correct but emphasizes the importance of including parentheses in the trees.
- Another participant confirms the results of tree traversals for one of the trees and expresses agreement with the findings.
- Some participants argue that one tree is correct while the other is incorrect, providing specific evaluations of the expressions represented by each tree.
- There is a discussion about the operator precedence and how it affects the evaluation of the expression, with references to the "biggest" operator being evaluated last.
- One participant mentions using Reverse Polish Notation and a calculator to assist in understanding the expression.
- Another participant seeks confirmation on the correctness of their traversal results for the tree deemed correct by others.
Areas of Agreement / Disagreement
Participants express disagreement regarding the correctness of the two trees, with some asserting that one tree is correct and the other is not. There is no consensus on the overall correctness of the trees, as multiple views are presented.
Contextual Notes
Limitations include potential misunderstandings of operator precedence and the representation of the algebraic expression in tree form. The discussion does not resolve these issues definitively.