- #1
etotheipi
Each node of a tree diagram corresponds to an event (i.e. a subset of the sample space), and the probability of the event at any node occurring equals the product of the probabilities along the path from the root to that node.
So considering the following two tree diagrams,
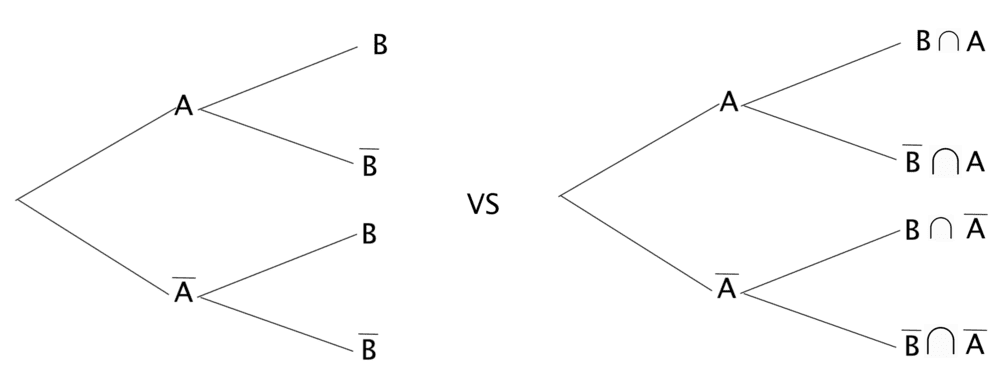
I would have thought the one on the right is correct, and the one on the left is wrong. Since on the left tree diagram, for instance, the top right node doesn't correspond to the event ##B## but the event ##A\cap B##. But I only ever see variants of the diagram on the left. My guess is that on the left only the last set in the compound event is written to save time? Or am I interpreting the tree structure in the wrong way?
On a slightly unrelated (more pedagogical) note, all of the undergrad level textbooks I've looked at don't have any tree diagrams. Is it the case that they're not used that much beyond school, since everything can be done more rigorously just with set notation?
So considering the following two tree diagrams,
I would have thought the one on the right is correct, and the one on the left is wrong. Since on the left tree diagram, for instance, the top right node doesn't correspond to the event ##B## but the event ##A\cap B##. But I only ever see variants of the diagram on the left. My guess is that on the left only the last set in the compound event is written to save time? Or am I interpreting the tree structure in the wrong way?
On a slightly unrelated (more pedagogical) note, all of the undergrad level textbooks I've looked at don't have any tree diagrams. Is it the case that they're not used that much beyond school, since everything can be done more rigorously just with set notation?