Kernel vector of statics Jacobian

In summary, the conversation discusses the use of a 3x4 statics Jacobian and the calculation of a kernel vector. The issue arises when using a 3x3 statics Jacobian, as removing a column would result in a non-square matrix and make it impossible to take the determinant. The person asks if there is another way to find the kernel vector or if the column should not be removed. They also mention using specialized terminology and suggest providing a link to the article or a relevant passage for clarification.
  • #1
aaddcc
9
0
Hi all,

I was reading an article that utilized a 3x4 statics Jacobian and said to calculate the kernel vector:
QVXCwFd.png
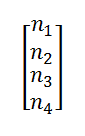You can row by row, where
L6af21V.png

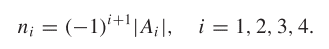
Where Ai is the statics Jacobian with the ith column removed. The problem is I have a 3x3 statics Jacobian, so if I remove the ith column I will end up with a non-square matrix, which means taking the determinant would not be possible. Is there another way to find the kernel vector in a similar way? Could I not remove the column?

Thanks!
 
Physics news on Phys.org
  • #2
You are using specialized terminology and it's unclear what your column vector represents. It would help if you gave a link to the article you mention or show a relevant passage from it. Are you working a problem in "statics", as in physics?
 

1. What is a kernel vector in the context of statics Jacobian?

A kernel vector is a vector that represents the set of all forces or torques that do not cause any motion in a given mechanical system. In other words, it is the set of forces and torques that are balanced and do not contribute to the overall motion of the system.

2. How is the kernel vector related to the statics Jacobian?

The kernel vector is directly related to the statics Jacobian, which is a matrix that describes the relationship between the external forces and torques acting on a mechanical system and the resulting motion. The kernel vector is the null space of the statics Jacobian, meaning it contains all the forces and torques that do not contribute to the motion described by the statics Jacobian.

3. What is the significance of the kernel vector in statics analysis?

The kernel vector is important in statics analysis because it allows us to identify the forces and torques that are essential for causing motion in a mechanical system. By removing the forces and torques in the kernel vector, we can simplify the analysis and focus on the significant external forces and torques that affect the motion of the system.

4. Can the kernel vector of statics Jacobian be used to determine the stability of a mechanical system?

Yes, the kernel vector can be used to determine the stability of a mechanical system. If the kernel vector is non-empty, it indicates that there are forces or torques that are balanced and do not cause any motion in the system. This means that the system is in a state of equilibrium and is potentially stable. On the other hand, if the kernel vector is empty, it indicates that there are no balanced forces or torques, and the system is not in equilibrium, which could lead to instability.

5. How is the kernel vector calculated in statics analysis?

The kernel vector can be calculated using linear algebra techniques such as matrix operations and eigenvalue analysis. It involves finding the null space of the statics Jacobian matrix, which can be done by finding the eigenvalues and eigenvectors of the matrix. The eigenvectors corresponding to the eigenvalue of 0 will form the kernel vector.

Similar threads

B How to multiply matrix with row vector?
    • Linear and Abstract Algebra
Replies
4
Views
1K
A Scaling And Reordering of Jacobian Free GMRES
    • Linear and Abstract Algebra
Replies
1
Views
1K
I Finding the Kernel of a Matrix Map
    • Linear and Abstract Algebra
Replies
11
Views
2K
I Vector subspace and basis vectors in the context of data science
    • Linear and Abstract Algebra
Replies
6
Views
869
B Is it invalid to redefine the sgn function in this way in a proof?
    • Linear and Abstract Algebra
Replies
15
Views
4K
I Solving simultaneous vector equations
    • General Math
Replies
11
Views
1K
MHB Is $s$ the unique vector that spans the solution space $L(A,0)$?
    • Linear and Abstract Algebra
Replies
3
Views
1K
A gardener collected 17 apples...
    • Precalculus Mathematics Homework Help
Replies
32
Views
835
I Rotational invariance of cross product matrix operator
    • Linear and Abstract Algebra
Replies
7
Views
2K
Vectors as geometric objects and vectors as any mathematical objects
    • Linear and Abstract Algebra
Replies
27
Views
1K

Hot Threads

Recent Insights

Back
Top