oddjobmj said:
Ah, thank you.
So you are saying that an easy way to get rid of the imaginary part is to leave the sin factor positive and plot between 0 and pi/2 instead of a negative sin and between pi and 3pi/2? I did finally work out the issue with my plot. The graph turned out similar to yours after I set the value inside the square root to negative.
Yes, it was what I suggested.
oddjobmj said:
edit: Also, between pi and 3pi/2 sin(theta) is not negative.
Well, what is sin (3pi/2) (sine of 270 degree)? or sin(4pi/3)? Do you remember the unit circle representation of the trigonometric functions? In which quadrants is sinθ negative?
oddjobmj said:
To make it negative under the square root I have to set the energy equation to this:
mgr=-.5v^2 m+mgr \sqrt{1-sin(θ)}
(note the tiny negative next to the kinetic energy component).
That is not correct, though. The initial potential should equal the sum of the potential and kinetic at a later point; not the difference. I'm just a bit confused about how to work the negative into a proper conservation of energy equation and why it needs to be negative.
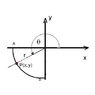
You are right, it is wrong. If you count theta from the positive x-axis as shown in the attached figure, the position of the mass at P is x=rcosθ , y=rsinθ.
Both cosθ and sinθ are negative, as P is in the third quadrant. When θ increases, y gets more negative and the potential decreases as the mass moves downward. If you take the potential energy equal to mgr at point A than it is
U=mg(r+y) = mgr(1+sinθ)
at point P and zero at point B.
Conservation of energy means that
1/2 mv^2+mgr(1+\sin\theta)=mgr
Rearranging the equation, mgr cancels and you get 1/2 mv^2+mgr\sin\theta=0
Isolate v: v=\sqrt{-2gr\sin\theta}, when θ changes from pi to 3pi/2.
oddjobmj said:
Also, I guess once I do end up with an estimated area under the curve I could just give the answer in terms of r by multiplying the variable r by the area, correct?
Lastly, I still don't understand why this form works for the estimation. dt/dθ is basically ω(t)-1. What is this plot representing? I'm sure I could get the answer correct at this point but I really want to make sense of it before moving on.
v is the speed and v= rω=rdθ/dt. So d\theta /dt = \sqrt{-\frac{2g}{r}\sin\theta}
θ(t) is function of the elapsed time, t. It is monotonous function in the range where pi≤θ≤3pi/2. The inverse function t(θ) exists in that interval and its derivative is dt/dθ, the reciprocal of the derivative of θ(t).
dt / d\theta = \frac{1}{\sqrt{-\frac{2g}{r}\sin\theta}}
The integral of dt/dθ from pi to 3pi/2 gives the elapsed time when the mass moves from point A to B. The area under the plot t(θ) between pi and 3pi/2 gives the elapsed time.
Note that r is under the square root. You can rearrange the equation to see how the time depends on r:
dt / d\theta = \frac{\sqrt{r}}{\sqrt{-2g\sin\theta}}
ehild