Kinematics: Solving for Position with Constant Velocity and Acceleration

Click For Summary

Homework Help Overview

The discussion revolves around a kinematics problem involving a car's motion with constant acceleration and deceleration. The scenario involves calculating the position at which a driver must switch from constant velocity to deceleration in order to stop at a designated road sign located at 100 m, starting from rest and with specified acceleration and deceleration rates.

Discussion Character

  • Exploratory, Assumption checking, Mathematical reasoning

Approaches and Questions Raised

  • Participants explore various kinematic equations and discuss the calculations for position and velocity at different stages of the car's motion. Questions arise regarding the correctness of results and alternative methods for verification. Some participants suggest working backwards from the stopping distance to find the necessary position to switch to deceleration.

Discussion Status

The discussion is active, with participants sharing calculations and questioning the validity of their results. Some guidance has been offered regarding the stopping distance and the relationship between time and constant velocity. Multiple interpretations of the problem setup are being explored, particularly concerning the transition points in the car's motion.

Contextual Notes

Participants note the constraints of the problem, including the need to calculate stopping distances and the relationships between different phases of motion. There is an acknowledgment of missing information regarding time values for certain segments of the journey.

Adriano25
Messages
40
Reaction score
4
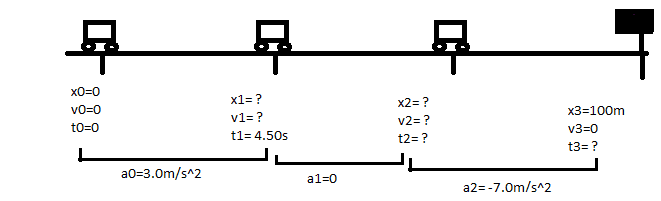
I've made a drawing in order to visualize the problem better:
car.png

1. Homework Statement
A car can increase its speed only at 3.00 m/s2, move at constant velocity, or decrease its speed at 7.00 m/s2. Starting at rest, the driver wishes to drive to a road sign located at x=100 m. He increases his speed, then travels at constant velocity and then decreasing his speed.
The driver begins accelerating at t=0 and switches to constant velocity at t=4.50 s. At what position must the driver switch from constant velocity to decreasing speed if he wants to stop the car at the road sign?

Homework Equations


These are the kinematic equations I used to solve the problem:
x1=x0+v0(t1-t0) + 1/2a0(t1-t0)2

v1=v0+a0(t1-t0)

v32=v22 + 2a2(x3-x2)

The Attempt at a Solution


x1=x0+v0(t1-t0) + 1/2a0(t1-t0)2
x1=1/2a0t12 =
x1=1/2(3.0m/s2)(4.50s)2 = 30.4m

v1=v0+a0(t1-t0)
v1=(3.0m/s2)(4.50s) = 13.5m/s

Since after v1 the velocity is constant, v2 must be constant and equal to 13.5m/s

v32=v22 + 2a2(x3-x2)
-v22=2a2x3-2a2x2
x2=-[-(v22-2a2x3) / 2a2]
x2 = -[(-182.25+1400)/-14] = 86.98m

Does this result look right?
 
Physics news on Phys.org
Adriano25 said:
86.98m

Does this result look right?

Can you think of a way to check? Perhaps you may see an easier way to do it.
 
PeroK said:
Can you think of a way to check? Perhaps you may see an easier way to do it.
I only see that I can skip the first step in finding x1, but I can't think of a way to check or find x2 in a different way. Any hints?
 
Adriano25 said:
I only see that I can skip the first step in finding x1, but I can't think of a way to check or find x2 in a different way. Any hints?

Work backwards. Think about stopping distance for the car.
 
PeroK said:
Work backwards. Think about stopping distance for the car.
Do you mean to check if x2 is equal to 86.98m or to find x2 in another way? The only way to check if x2 is equal to 86.98m is to use the same formula I used to find this value which is:
v32=v22+ 2a2(x3-x2)
Since we don't have any values for t3 or t2

Also, in order to find x2 working backwards, I think I still need to find v2 first. I'm a little confused. Perhaps I'm missing some relationship in between time and constant velocity.
 
Adriano25 said:
Do you mean to check if x2 is equal to 86.98m or to find x2 in another way? The only way to check if x2 is equal to 86.98m is to use the same formula I used to find this value which is:
v32=v22+ 2a2(x3-x2)
Since we don't have any values for t3 or t2

Also, in order to find x2 working backwards, I think I still need to find v2 first. I'm a little confused. Perhaps I'm missing some relationship in between time and constant velocity.

Suppose the car is moving along at ##13.5 ms^{-1}##. It has a fixed deceleration of ##7ms^{-2}##. From that you can calculate the stopping distance of the car. Once you know the stopping distance, you can subtract that from ##100m##.
 
The only way I can think of based on the formulas I learned would be subtracting x2-x1. So it would be 86.98m-30.4m=50.6m
However, I don't understand this approach because based on my sketch I uploaded on the first post, I set x2 as the position in which the driver must switch from constant velocity to decreasing speed if he wants to stop the car at the road sign.
 
Adriano25 said:
The only way I can think of based on the formulas I learned would be subtracting x2-x1. So it would be 86.98m-30.4m=50.6m
However, I don't understand this approach because based on my sketch I uploaded on the first post, I set x2 as the position in which the driver must switch from constant velocity to decreasing speed if he wants to stop the car at the road sign.

What about this question:

A car is moving along at ##13.5 ms^{-1}##. It has a fixed deceleration of ##7ms^{-2}##.

a) How long does it take to stop (time)?
b) How far does it travel before it stops?

Can you work that out?
 
PeroK said:
What about this question:

A car is moving along at ##13.5 ms^{-1}##. It has a fixed deceleration of ##7ms^{-2}##.

a) How long does it take to stop (time)?
b) How far does it travel before it stops?

Can you work that out?
Yes.
a)
v1=v0+a0(t1-t0)
t1=1.93 s

b)
v12=v02+2a0(x1-x0)
-182.25=-14x1
x1=13.02 m
 
  • #10
Adriano25 said:
Yes.
a)
v1=v0+a0(t1-t0)
t1=1.93 s

b)
v12=v02+2a0(x1-x0)
-182.25=-14x1
x1=13.02 m

So, you need to start decelerating ##13.02m## before the point you want to stop. And what is ##100m - 13.02m##?
 
  • #11
PeroK said:
So, you need to start decelerating ##13.02m## before the point you want to stop. And what is ##100m - 13.02m##?
So 100m - 13.02m = 86.98 m would be the position in which the driver must switch from constant velocity to decelerating in order to stop the car at 100m correct?
 
  • #12
Adriano25 said:
So 100m - 13.02m = 86.98 m would be the position in which the driver must switch from constant velocity to decelerating in order to stop the car at 100m correct?

Yes, exactly. And now you have a much simpler solution to the original problem.
 
  • #13
Great. Thanks for your help!
 

Similar threads

Kinematic problem, are my variables right,
  • · Replies 34 ·
2
Replies
34
Views
3K
Jet accelerating in problem with Constant Acceleration
  • · Replies 10 ·
Replies
10
Views
2K
1D Angular Motion with different velocity stages
  • · Replies 3 ·
Replies
3
Views
2K
Kinematics problem, is it possible to solve with given information?
  • · Replies 11 ·
Replies
11
Views
3K
Finding Initial Velocity v0x for Particle with Non-Constant Acceleration
  • · Replies 2 ·
Replies
2
Views
4K
Classical mechanics problem for a free particle
  • · Replies 2 ·
Replies
2
Views
2K
Calculating impact velocity of freefalling object with increasing grav
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Best way to measure velocity, acceleration and jerk
  • · Replies 1 ·
Replies
1
Views
2K
How Do You Solve a Kinematics Tennis Ball Problem Using d-v-a-t Formulas?
  • · Replies 1 ·
Replies
1
Views
2K
How to interpret the equation of position with constant acceleration?
  • · Replies 11 ·
Replies
11
Views
2K