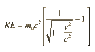Kinetic Energy Needed for Proton Acceleration

[fatcats]

Homework Statement

a) Calculate the kinetic energy required to accelerate a single proton from a rest position to 0.9999c. The mass of a proton is 1.67*10^-27 kg.
b) Find the ratio of the kinetic energy to the energy of a proton at rest.
c) Explain why no particle accelerator will ever be able to accelerate any particle to the speed of light.

Homework Equations

a) Ek = Etotal - Erest

Ek = mc^2/sqroot 1 - v^2/c^2 - mc^2

b) Ek/Erest

The Attempt at a Solution

a) I am including the calculations I have done on my word document page to make it more legible than typing it in here. Please see the attached image.

I think my work is right, but I have cross-referenced this answer with others and the math does not seem to be right... it seems to be correct until at least the step where:

Ek = 1.50 * 10^-10 / sqroot(1.9999*10^-4) - 1.50 *10^-10

After that I am not sure, but the answer I keep getting is 9.11 * 10^-10, and other answers, deemed correct have a totally different number multiplied by 10^-8...
I have been reworking this and trying to figure out where/if my calculation is wrong and I'm stuck.

b) For this question, all I do is divide the two numbers for the ratio, correct? This question is worth three marks and it seems like they want something more than just this? Am I missing something?

c) Not sure how to word this. Here's my best attempt. This question is worth one mark.

No particle accelerator will ever be able to accelerate any particle to the speed of light because according to the denominator of the aforementioned equation, sqroot (1-v^2/c^2), the speed of light acts as a limit to velocity. If velocity were to equal the speed of light, then there would be no difference in resting and kinetic energies.

Please help me understand, I am doing this course online and don't really have a teacher who can help me out. Thanks for your time.

 

[mjc123]

In your penultimate step you have divided by 0.141... instead of 0.0141...

If velocity were to equal the speed of light, then there would be no difference in resting and kinetic energies.

No - if velocity = c, then KE is infinite.

 

[fatcats]

Oh! Is that my only mistake with calculations? Thank you so much.

Why is KE infinite with velocity = c? Wouldn't that make the denominator 1? I don't understand

 

[berkeman]

Why is KE infinite with velocity = c? Wouldn't that make the denominator 1? I don't understand

It's hard to read your equations -- consider learning to use LaTeX for your equations when posting at the PF. There is a LaTeX Primer under INFO (at the top of the page), Help/How-To.

When written out as an equation, it's easy to see how the denominator goes to zero if v = c

http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/imgrel/rke2.gif

 

[fatcats]

I usually upload my equations in a neat screenshot, but I will look at Latex

I don't understand why it is infinity.

(c)^2/(c)^2 = 1
1 - (c)^2/(c)^2 = 0
squareroot of 0 = 0

so how is that infinity?

 

[berkeman]

I usually upload my equations in a neat screenshot, but I will look at Latex

I don't understand why it is infinity.

(c)^2/(c)^2 = 1
1 - (c)^2/(c)^2 = 0
squareroot of 0 = 0

so how is that infinity?

The zero is in the denominator...

 

[fatcats]

Yes, I understand that, but how does dividing by zero make it infinity? Doesn't that make a number undefined?

I was always taught that means it's unsolvable

 

[berkeman]

Yes, I understand that, but how does dividing by zero make it infinity? Doesn't that make a number undefined?

I was always taught that means it's unsolvable

Well that may be true (I'm not a math expert), but think about what the value of that fraction does as v --> c from below. The KE rises without bound, right? That's the point, that the KE increases without bound as you try to get closer and closer to c (at least when you approach it from speeds v < c).

 

[fatcats]

Okay, I think I understand
If you look at it as an equation, it's harder to see, but if you visualize it at as a graph that makes sense to me
Thanks for your help!