KRC
- 1
- 0
Homework Statement
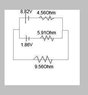
At what rate is electrical energy converted to internal energy in the 4.56Ω and the 5.91Ω resistors in the figure?
Homework Equations
Kirchoff's Laws:
ƩI(in) = ƩI(out) Junction Rule
ƩΔV = 0 Loop Rule
The Attempt at a Solution
I have set the top branch current to go from right to left = I(3)
I have set the middle branch current to go from right to left = I(2)
I have set the bottom branch current to go from left to right = I(1)
The left middle junction results in the following I(3) + I(2) = I(1)...Junction#1
Loop #1 = 0 = 6.96V-5.91I(2)-4.56I(3)
Loop #2 = 0 = -9.56I(1)-5.91I(2)+1.86V
I get I1=2.7502
I2=-4.1340
I3=6.8842
The answers I get when using the P=I^(2)*R...do not yield results consistent with the online homework
I have tried this several different ways and the answer according to my homework do not match. Please provide some insight here.
Thank You.