- #1
AdrianZ
- 319
- 0
I encountered this beautiful theorem and then I tried hard to prove it using ordinary algebraic methods and my understanding of calculus without involving real analysis in it but I didn't succeed. The theorem states that if f is an analytical function at some point x=a then f-1 has the following Taylor series:
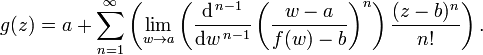
How can I prove this formula?
How can I prove this formula?