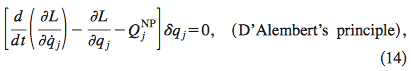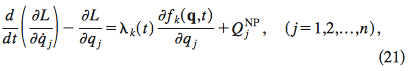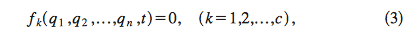Lagrange multiplier in Hamilton's and D'Alembert's principles

[Happiness]

Why do displaced paths need to satisfy the equations of constraint when using the method of Lagrange multiplier? I thought that with the multiplier, all the coordinates are free and hence should not be required to satisfy the equations of constraint.

Source: http://www.phys.ufl.edu/~maslov/classmech/flannery.pdf

 

[vanhees71]

No, not for really nonholonomic constraints. There you have more degrees of freedom for large displacements than for infinitesimal ones, and you cannot integrate the infinitesimal ones to holonomic constraints, because the corresponding form is not a total differential. Think about the example with the skate on an inclined plane. This seems to be the most simple example for a truly nonholonomic system.

 

[Happiness]

No, not for really nonholonomic constraints. There you have more degrees of freedom for large displacements than for infinitesimal ones, and you cannot integrate the infinitesimal ones to holonomic constraints, because the corresponding form is not a total differential. Think about the example with the skate on an inclined plane. This seems to be the most simple example for a truly nonholonomic system.

The reason given for why we can't use Lagrange multiplier in non-holonomic constraint is that the varied paths do not satisfy the equation of constraint. I do not understand this reason. I would think that only the actual path needs to satisfy the equation of constraint and the varied path can be any path as long as it has the same end points.

 

[Happiness]

The method of Lagrange multipliers can be used to transform an $m$-dimensional variational problem A with $c$ equations of constraint into an $(m+2c)$-dimensional variational problem B without any constraint. Why Lagrange multipliers can't be used for non-holonomic constraints is, I believe, because of a way simpler reason. It is not because the method can't transform variational problem A into variational problem B when non-holonomic constraints are present, but rather, it is because variational problem A does not exist! Hence, there is no place for us to use Lagrange multipliers.

In order for variational problem A to exist, we must be able to vary a trajectory $q(t)$ and look for the trajectory that gives the action $J=\int_{t_1}^{t_2}L(q,\dot{q},t)\,dt$ a stationary value. For a problem with constraint, that would mean that we look for such a trajectory from a set of constraint-satisfying trajectories. When the constraint is non-holonomic, varying a constraint-satisfying trajectory slightly, in general, produces a trajectory that is not constraint-satisfying. Hence, any constraint-satisfying trajectory exists in isolation in general, as a curve separated from other constraint-satisfying trajectories instead of joining up with them to form a continuous surface. The problem immediately becomes non-variational in nature, i.e., variational problem A does not exist. In fact, the phrase "to make $J$ stationary" does not even make sense.

 

[vanhees71]

The reason given for why we can't use Lagrange multiplier in non-holonomic constraint is that the varied paths do not satisfy the equation of constraint. I do not understand this reason. I would think that only the actual path needs to satisfy the equation of constraint and the varied path can be any path as long as it has the same end points.

Of course, you use Lagrange multipliers, but not as part of the Lagrangian but as part of the variation of the action. So let's do it again. Suppose we have given our problem in terms of generalized coordinates $(q^k)$, $k \in \{1,\ldots,f \}$ and suppose we have only proper nonholonomic constraints. This means we have $r<f$ constraints on the virtual displacements,
$$\delta q^k f_k^{(\alpha)}(t,q)=0, \quad \alpha \in \{1,2,\ldots,r \}$$
which cannot be integrated to holonomic constraints. In other words we suppose we have already solved for all holonomic constraints in choosing our $f$ generalized coordinates. This means the functions $f_k^{(\alpha)}$ are such that
$$\partial_j f_k^{(\alpha)}-\partial_k f_j^{(\alpha)} \neq 0.$$
In this case we cannot vary the $q^k$ independently in Hamilton's principle of stationary action, but we have to fulfill the constraints. This can be done by introducing $r$ Lagrange multipliers $\lambda_{\alpha}$ and vary the $q^k$ and the $\lambda^{\alpha}$ independently. The variation of the extended action then reads
$$\delta S=\int \mathrm{d} t \delta q^k \left (\frac{\partial L}{\partial q^k}-\frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{q}^k}+\lambda_{\alpha} f_k^{(\alpha)} \right) \stackrel{!}{=} 0.$$
The equations of motion thus read
$$\frac{\partial L}{\partial q^k}-\frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{q}^k}+\lambda_{\alpha} f_k^{(\alpha)} =0, \quad f_k^{(\alpha)} \dot{q}^k=0.$$
Note that Einstein's summation convention is understood here, for both the summation over $k \in \{1,\ldots,f \}$ and $\alpha \in \{1,\ldots,r \}$. Now you have $(k+r)$ functions $q^k(t)$ and $\lambda_\alpha(t)$ to solve for and also $k$ Lagrange Equations of the 1st kind and the $r$ constraint equations.