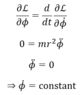Lagrangian and Equations of Motion for Conical Pendulum

[Mason Smith]

Homework Statement

Consider a conical pendulum. This is a simple pendulum that, instead of swinging back and forth through an equilibrium point, traces out a right circular cone.

Relevant Equations

The Lagrangian is defined as the difference of the kinetic energy T and the potential energy U.
Lagrange's equations say that the partial derivative of the Lagrangian with respect to some generalized coordinate is equal to the time derivative of the partial derivative of the Lagrangian with respect to the time derivative of some generalized coordinate.

Here is a picture of the problem.

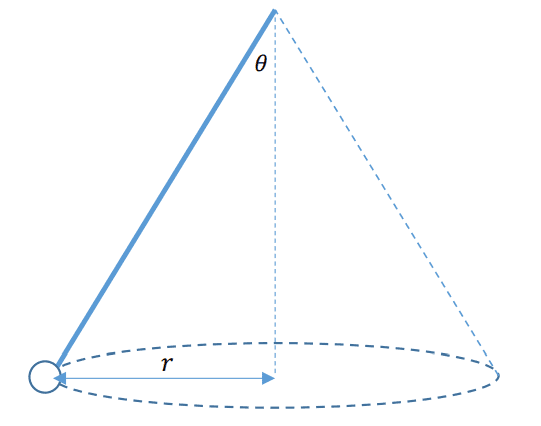
I have chosen the origin to lie in the middle of the circle around which the mass moves. I have also chosen the z axis to pass through the origin and through the vertex of the right circular cone. The x-axis and y-axis are so that one when curls his or her fingers from the x-axis to the y axis, the thumb of the right hand will point in the direction of the z axis. Since the mass lies in the xy plane, I have defined the potential energy U to be zero. This leads to

.
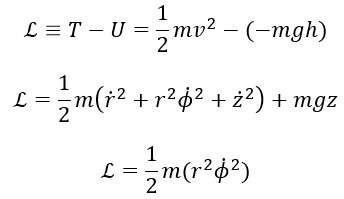Applying Lagrange's equations,

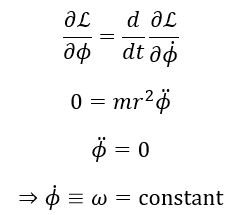
where ω is the angular velocity.
While this result is convenient, it leads me to question its correctness. If I have made a mistake anywhere, then can anyone please point me in the correct direction for analyzing the motion of the mass? Thanks in advance! :)

 

[Abhishek11235]

This is alright. One way to check correctness is to double check your answer with Newton's laws(whenever possible)

 

[wrobel]

So you have proved that for each $\theta=const$ the particle can rotate in horizontal plane with arbitrary speed . The solution is wrong. Spherical pendulum is a system with two degrees of freedom. You must write two Lagrangian equations first and only after that find particular solutions. Instead that you solve this problem as if it has an additional constraint $\theta=const$