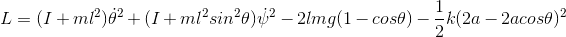dynamicskillingme
- 26
- 0
Homework Statement
Homework Equations
L = T-V
The Attempt at a Solution
I got a formula for the lagrangian as
The forum discussion centers on deriving the Lagrangian for a centrifugal regulator, specifically using the formula L = T - V, where T represents kinetic energy and V represents potential energy. Participants emphasize the importance of including rotational kinetic energy terms and correcting the gravitational potential energy component. Key issues identified include the need to account for the rotational inertia of the spheres and the correct interpretation of the distance from the pivot to the center of mass. The conversation concludes with a participant expressing gratitude for assistance in refining their Lagrangian formulation.
PREREQUISITESStudents and professionals in physics, particularly those focusing on classical mechanics, as well as engineers working with dynamic systems and control mechanisms.
check the L written above and set up the Lagrange's equations of motion...dynamicskillingme said:I got a formula for the lagrangian as

Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.drvrm said:check the L written above and set up the Lagrange's equations of motion...
dynamicskillingme said:Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.
dynamicskillingme said:Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.
You have neglected the rotational inertia of the spheres about their centers. This will add additional terms to T. Also, check the sign of the gravitational potential energy part of L.dynamicskillingme said:Its more I don't know if the L is correct and wanted to check what the derivation is with someone else's because I'm pretty sure my derivation is wrong.
Each ball does rotate as either ##\theta## or ##\psi## changes. Consider a ball attached to the end of a stick as shown in the figure below. As the stick rotates through an angle θ, the ball also rotates through θ.dynamicskillingme said:I don't believe the balls are allowed to rotate about their centers.
The potential energy is subtracted in the Lagrangian: L = T - V. You got the sign correct for the spring potential energy.Why wouldn't the gravitational potential be positive?
It's just a kinetic energy term due to rotation about the center of mass.dynamicskillingme said:Yeah I agree with that, but what other term would that introduce?
If θ increases, both the spring potential energy and the gravitational potential energy increase.Also wouldn't the gravity term be the opposite direction to the spring?
dynamicskillingme said:Could you possibly write out the correct Lagrangian as I feel like I'm stumbling around it and would love to inspect the correct one. And sorry there is a note at the start of my work I forgot and it just says
That's getting very close to the correct ##L##. However, you need to include a rotational KE term associated with ##\dot{\theta}## as well as with ##\dot{\psi}##. And, as you say, the coefficient for the gravity terms needs to be corrected.dynamicskillingme said: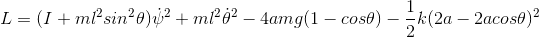
When evaluating ##\frac{\partial{L}}{\partial \theta}##, how did you get factors of ##\dot{\theta}## to appear?
This expression for ##L## looks correct to me as long as the distance ##l## has the correct interpretation.dynamicskillingme said: