Laplace Transform and complex contours

[saltydog]

In the HW section, the following equation was proposed:

ty(t)=\int_0^t \tau^{1-\alpha}y(t-\tau)d\tau;\quad \int_0^\infty y(x)dx=1

Link to HW thread: https://www.physicsforums.com/showthread.php?t=97562

Using Laplace Transforms:

Y(p)=\mathcal{L}\left\{y(t)\right\}

and noting the RHS is the inverse transform of a convolution, we obtain the IVP:

-Y^{'}=Y\frac{\Gamma(\alpha)}{p^\alpha};\quad Y(0)=\int_0^\infty e^{-0t}y(t)dt=1

solving for \alpha \ne 1:

Y(p)=Exp\left[-\frac{\Gamma(\alpha)}{1-\alpha}s^{1-\alpha}\right]

I (Mathematica) can invert this only for \alpha=1/2:

y(t)=\frac{e^{-\pi/t}}{t^{3/2}}

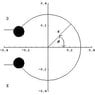
I'd like to know how to invert it for other values of alpha. My only recourse is to evaluate the complex contour for the inverse transform:

\frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty} Y(p)e^{pt}dp

I'm not too good at this. I know I need to learn more about Complex Analysis and contours specifically, but for the time being, can someone help me through the integral for alpha=1/2:

\frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty} \frac{e^{st}}{e^{2\sqrt{\pi s}}}ds=\frac{e^{-\pi/t}}{t^{3/2}}

 

[Tide]

Briefly: Make a change of variables using s = \sigma^2, complete the square in the exponential, scale out the t (which gives you the scaling of t^{-3/2} immediately) and note that the change of variables requires your new contour to asymptote to the lines e^{i \pi / 4} and e^{-i \pi / 4}. It should be apparent that you're dealing with the Fresnel integral functions with the usual results.

 

[saltydog]

Briefly: Make a change of variables using s = \sigma^2, complete the square in the exponential, scale out the t (which gives you the scaling of t^{-3/2} immediately) and note that the change of variables requires your new contour to asymptote to the lines e^{i \pi / 4} and e^{-i \pi / 4}. It should be apparent that you're dealing with the Fresnel integral functions with the usual results.

Thanks Tide. I'll work with it. May take a while.

 

[saltydog]

Briefly: Make a change of variables using s = \sigma^2, complete the square in the exponential, scale out the t (which gives you the scaling of t^{-3/2} immediately) and note that the change of variables requires your new contour to asymptote to the lines e^{i \pi / 4} and e^{-i \pi / 4}. It should be apparent that you're dealing with the Fresnel integral functions with the usual results.

Tide, it's not happening for me. Doing as you suggest, (completing the square), I get:

2e^{-\pi/t^2}\int e^{t(u-\frac{\sqrt{\pi}}{t})^2}udu

I don't see where to go from there and I really don't understand how the limits are changed as you suggest.

But I know where my problem lies and I know how to correct it: I don't have a sufficient understanding of Complex Analysis to even ask the question, and in order to approach this problem I would first have to work on other more simple problems. That's Ok. I have the time.

I did however go to the Library today and searched several tables of inverse transforms. It turns out that only for the case of alpha=1/2 is an inverse transform published. I suspect then even when I do master the contour integral, a closed-form solution for other values of alpha will NOT be attainable and thus I will have to resort to numerical methods of computing the inverse transforms. I know absolutely nothing about such numerical methods but I'm interested in learning about them and arriving at a complete solution of this problem in terms of alpha.

I also purchased a book on Complex Analysis and will take my own advice in here: Start on page 1.

 

[Tide]

salty,

I just went through the transformations and I get

\frac {2 e^{-\pi / t}}{t^{3/2}} \int e^{\left( \sigma - \sqrt {\pi / t}\right)^2} \sigma d\sigma

The original contour for the inverse Laplace transform effectively goes from R e^{-i\pi/2} to R e^{i\pi/2} with R \rightarrow \infty. Since \sigma = \sqrt s the new limits will be from \sqrt R e^{-i\pi/4} to \sqrt R e^{i\pi/4}. Looking at it more carefully shows one more change of variables is needed (a translation) to simplify the argument of the exponential.

When you're all one with that, you should have the integral I suggested in my previous post. For now you just have to go back and recheck your transformations.

 

[Tide]

P.S. I didn't include the factor \frac {1}{2\pi i} in my previous post.

 

[saltydog]

salty,
I just went through the transformations and I get
\frac {2 e^{-\pi / t}}{t^{3/2}} \int e^{\left( \sigma - \sqrt {\pi / t}\right)^2} \sigma d\sigma

Tide, I cannot arrive at the answer you propose and when I check the integral with real values, your substitution does not lead to the numerical answer:

Let's just for now consider a real integral and let t=3:

\int_0^1 \frac{e^{st}}{e^{2\sqrt{\pi s}}}ds

when I numerically integrate this I obtain:

\int_0^1 \frac{e^{st}}{e^{2\sqrt{\pi s}}}ds\approx 0.428599

When I let:

\sigma^2=s

then the limits in \sigma are the same.

Completing the square as you suggest, I arrive at:

2e^{-\pi/t}\int_0^1 e^{t(\sigma-\sqrt{\pi}/t)^2}\sigma d\sigma

numerically integrating that I obtain the same result as above. However, when I numerically integrate your solution:

\frac {2 e^{-\pi / t}}{t^{3/2}} \int_0^1 e^{\left( \sigma - \sqrt {\pi / t}\right)^2} \sigma d\sigma

I obtain 0.0830375. I suspect I'm making a dumb mistake and can handle you correcting me.

 

[Tide]

salty,

There are two problems. First, I didn't do the transformations quite right so the t^(3/2) should just be t:

\frac {2 e^{-\pi / t}}{t} \int e^{\left( \sigma - \sqrt {\pi / t}\right)^2} \sigma d\sigma

Also, if you want do a numerical comparison you have to set the limits properly. Remember, there was a scaling that eliminated the factor of t from the exponential which looks like \sigma = \sqrt {t} \sigma' so if you set t = 3 then the upper limit in the transformed integral will be \sqrt {3}.

 

[saltydog]

Tide,

As you requested, I've achieved oneness with the integral. Here it is with your substitutions in case others are following this:

Above, after letting:

\sigma^2=s

and completing the square, we obtain:

2e^{-\pi/t}\int e^{t(\sigma-\sqrt{\pi}/t)^2}\sigma d\sigma

Now, in order to remove the t in the exponent, we let:

v=\sqrt{t}\sigma

so that:

dv=\sqrt{t}d\sigma,\quad \sigma=\frac{v}{\sqrt{t}},\quad d\sigma=\frac{dv}{\sqrt{t}}

Substituting this scalling factor into the exponent:

<br /> \begin{align*}<br /> t\left[\frac{v^2}{t}-\frac{2v\sqrt{\pi}}{t\sqrt{t}}+\frac{\pi}{t^2}\right]&amp;=<br /> v^2-2v\sqrt{\pi/t}+\frac{\pi}{t} \\<br /> &amp;=(v-\sqrt{\pi/t})^2<br /> \end{align}<br />

substituting this into the integral:

2e^{-\pi/t}\int e^{(v-\sqrt{\pi/t})^2}\left(\frac{v}{\sqrt{t}}\right)\frac{dv}{\sqrt{t}}

Simplifying:

\frac{2e^{-\pi/t}}{t}\int e^{(v-\sqrt{\pi/t})^2}vdv;\quad v=\sqrt{t}\sigma;\quad \sigma^2=s

I'll start working with the complex analysis part . . .

 

[saltydog]

Tide, anyone else too you know, can you please review the analysis below and let me know if I understand it so far. Thanks!

The original integral was:

\int_{\gamma-i\infty}^{\gamma+i\infty} \frac{e^{st}}{e^{2\sqrt{\pi s}}}ds

This can be re-written as:

\mathop\lim\limits_{y\to\infty}\int_{\gamma-yi}^{\gamma+yi} \frac{e^{st}}{e^{2\sqrt{\pi s}}}ds

Gamma is taken to be ANY positive constant such that the contour is to the right of any singularities of the integrand. I believe the integrand is entire so we can just take gamma to be 1. Converting to polar coordinates, the upper and lower limits become:

s_1=1-yi=Re^{-i\theta}

s_2=1+yi=Re^{i\theta}

Now, as y goes to infinity, theta approaches pi/2 and R goes to infinity. In the first transformation we had:

\sigma^2=s

Thus in terms of sigma, the limits become:

\sigma_1=\sqrt{Re^{-\pi i/2}}=\sqrt{R}e^{-\pi i/4}

\sigma_2=\sqrt{Re^{\pi i/2}}=\sqrt{R}e^{\pi i/4}

with R approaching infinity.

In the second transformation, we have:

v=\sqrt{t}\sigma

In terms of v, then the limits become:

v_1=\sqrt{Rt}e^{-\pi i/4}

v_2=\sqrt{Rt}e^{\pi i/4}

Thus arriving at the final form of the inverse transform:

y(t)=\frac{1}{2\pi i}\frac{2e^{-\pi/t}}{t}\mathop\lim\limits_{R\to\infty}\int_{\sqrt{Rt}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}} e^{(v-\sqrt{\pi/t})}^2vdv

I've already done some preliminary calculations of the integral and the results do indeed tend to the desired result:

y(t)=\frac{e^{-\pi/t}}{t^{3/2}}

However I cannot yet provide a proof and plan to work on this next.

 

[saltydog]

For the following:

y(t)=\frac{1}{2\pi i}\frac{2e^{-\pi/t}}{t}\mathop\lim\limits_{R\to\infty}\int_{\sqrt{RT}e^{-\pi i/4}}^{\sqrt{RT}e^{\pi i/4}} e^{(v-\sqrt{\pi/t})}^2vdv

First consider:

\int e^{(x-k)^2} xdx

Letting:

u=x,\quad dv=e^{(x-k)^2}dx

so that:

du=dx,\quad v=\frac{\sqrt{\pi}}{2}\text{Erfi}(x-k)

where:

\text{Erfi}(z)=\frac{\text{Erf}(iz)}{i}

and therefore:

\int e^{(x-k)}^2 xdx=x\frac{\sqrt{\pi}}{2}\text{Erfi}(x-k)-\frac{\sqrt{\pi}}{2}\int \text{Erfi}(x-k)dx

Now:

\int \text{Erfi}(x-k)dx=\frac{1}{\sqrt{\pi}}e^{(x-k)^2}-k\text{Erfi}(x-k)+x\text{Erfi}(x-k)

and thus:

\int e^{(x-k)^2}xdx=\frac{\sqrt{\pi}}{2}\left[\frac{e^{(x-k)^2}}{\sqrt{\pi}}+k\text{Erfi}(x-k)\right]

Therefore if we let:

k=\sqrt{\pi/t}

we obtain:

\int e^{(v-\sqrt{\pi/t})^2}vdv=\frac{\sqrt{\pi}}{2}\left[\frac{e^{(v-\sqrt{\pi/t})^2}}{\sqrt{\pi}}+\sqrt{\pi/t}\text{Erfi}(v-\sqrt{\pi/t})\right]

This then reduces the inverse transform to the following expression:

y(t)=\frac{e^{-\pi/t}}{2\pi i t}\left[\mathop\lim\limits_{R\to\infty}\left(e^{(v-\sqrt{\pi/t})^2}+\frac{\pi}{t^{1/2}}\text{Erfi}(v-\sqrt{\pi/t})\right)_{\sqrt{Rt}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}}\right]

Edit: Oh yea: Equal rights for special functions.

 

[saltydog]

I wish to analyze:

y(t)=\frac{e^{-\pi/t}}{2\pi i t}\left[\mathop\lim\limits_{R\to\infty}\left(e^{(v-\sqrt{\pi/t})^2}+\frac{\pi}{t^{1/2}}\text{Erfi}(v-\sqrt{\pi/t})\right)_{\sqrt{Rt}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}}\right]

in two parts.

First consider the limit of the first term:

\mathop\lim\limits_{R\to\infty}\left[e^{(v-\sqrt{\pi/t})^2}\right]_{\sqrt{RT}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}}

Converting the upper limit to polar form:

<br /> \begin{align*}<br /> \sqrt{Rt}e^{\pi i/4}&amp;=\sqrt{Rt}\left(Cos(\pi/4)+iSin(\pi/4)\right) \\<br /> &amp;=\sqrt{\frac{Rt}{2}}+i\sqrt{\frac{Rt}{2}}<br /> \end{align}<br />

so that:

<br /> \begin{align*}<br /> (v-\sqrt{\pi/t})^2&amp;=\left[\left(\sqrt{Rt/2}-\sqrt{\pi/2}\right)+i\sqrt{Rt/2}\right]^2 \\<br /> &amp;=\left(-2\sqrt{Rt/2}+\pi/t\right)+i\left(Rt-2\sqrt{R\pi/2}\right)<br /> \end{align}<br />

The upper limit then becomes:

\mathop\lim\limits_{R\to\infty} Exp\left[\left(-2\sqrt{R\pi/2}+\pi/t\right)+i\left(Rt-2\sqrt{R\pi/2}\right)\right]

Note the real part of the expression is negative and as R goes to infinity, the coefficient on the Euler expansion goes to zero and thus the limit is zero.

The same analysis can be made for the lower limit. This limit is therefore zero. We can now write the inverse transform as:

y(t)=\frac{e^{-\pi/t}}{2\pi i t}\mathop\lim\limits_{R\to\infty}\left\{\frac{\pi}{t^{1/2}}\text{Erfi}\left(v-\sqrt{\pi/t}\right)_{\sqrt{Rt}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}}\right\}

or:

y(t)=\frac{e^{-\pi/t}}{2 i t^{3/2}}\mathop\lim\limits_{R\to\infty}\left\{\text{Erfi}\left(v-\sqrt{\pi/t}\right)_{\sqrt{Rt}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}}\right\}

 

[saltydog]

I wish to finally evaluate:

<br /> y(t)=\frac{e^{-\pi/t}}{2 i t^{3/2}}\mathop\lim\limits_{R\to\infty}\left\{\text{Erfi}\left(v-\sqrt{\pi/t}\right)_{\sqrt{Rt}e^{-\pi i/4}}^{\sqrt{Rt}e^{\pi i/4}}\right\}\tag{1}<br />

First note:

<br /> \text{Erfi}(z)=\frac{\text{Erf(iz)}}{i}=\frac{1}{i}\frac{2}{\sqrt{\pi}}\int_0^{iz} e^{-w^2}dw<br />

Using this relation, I can re-write the above limit as:

<br /> \frac{2}{i\sqrt{\pi}}\left\{\mathop\lim\limits_{R\to\infty}\int_0^{i(\sqrt{Rt}e^{\pi i/4})} e^{-w^2}dw-\mathop\lim\limits_{R\to\infty}\int_0^{i(\sqrt{Rt}e^{-\pi i/4})} e^{-w^2}dw\right\}<br />

Using Euler's relation, I convert the upper limits to real and imaginary parts and multiply by i:

<br /> \begin{align*}<br /> i\sqrt{Rt}e^{\pi i/4}&amp;=i\left[\left(\sqrt{Rt/2}-\sqrt{\pi/2}\right)+i\sqrt{Rt/2}\right] \\<br /> &amp;=-\sqrt{Rt/2}+i\left(\sqrt{Rt/2}-\sqrt{\pi/t}\right)<br /> \end{align}<br />

Now, as R goes to infinity, this quantity goes to -\infty+i\infty.

And the lower limit:

<br /> \begin{align*}<br /> i\sqrt{Rt}e^{-\pi i/4}&amp;=i\left[\sqrt{Rt/2}+\left(\sqrt{Rt/2}-\sqrt{\pi/2}\right)\right] \\<br /> &amp;=\sqrt{Rt/2}+i\left(\sqrt{Rt/2}-\sqrt{\pi/2}\right)<br /> \end{align}<br />

as R goes to infinity, this limit goes to \infty+i\infty.

Thus the integrals can be rewritten as:

<br /> \frac{1}{i}\frac{2}{\sqrt{\pi}}\int_0^{-\infty+i\infty} e^{-w^2}dw-<br /> \frac{1}{i}\frac{2}{\sqrt{\pi}}\int_0^{\infty+i\infty} e^{-w^2}dw<br />

I choose to evaluate these line integrals along a parametric path using the following relation from Complex Analysis:

<br /> \int_C f(z)dz=\int_c udx-vdy+i\int_c vdx+udy<br />

Thus the first step is to express the integrand in terms of a real and imaginary part. Relying on Euler's formula:

<br /> \begin{align*}<br /> e^{-w^2}&amp;=e^{-(x+yi)^2} \\<br /> &amp;=e^{-(x^2-y^2+2xyi)} \\<br /> &amp;=e^{-(x^2-y^2)}Cos(2xy)+ie^{-(x^2-y^2)}(-Sin(2xy))\\<br /> &amp;=u+iv<br /> \end{align}<br />

For the first integral, the path goes from the origin to the point -\infty+i\infty

Thus if I let:

x=-t,\quad dx=-dt

y=t,\quad dy=dt

Making this substitution, note that the exponent term is 1 and we have for the first integral (with t going from 0 to infinity):

<br /> \begin{align*}<br /> \int_0^{-\infty+i\infty} e^{-w^2}dw&amp;=\left(-\int_0^\infty Cos(-2t^2)dt+\int_0^\infty Sin(-2t^2)dt\right) \\<br /> &amp;+i\left(\int_0^\infty Cos(-2t^2)dt+\int_0^\infty Sin(-2t^2)dt\right) \\<br /> &amp;=\left(-\frac{\sqrt{\pi}}{4}-\frac{\sqrt{\pi}}{4}\right)+i\left(\frac{\sqrt{\pi}}{4}-\frac{\sqrt{\pi}}{4}\right) \\<br /> &amp;=-\frac{\sqrt{\pi}}{2}<br /> \end{align}<br />


The same analysis can be made (with the path going from 0 to \infty+i\infty for the second integral with the results that the line integral in that case is:

<br /> \frac{\sqrt{\pi}}{2}

Substituting these values into (1), I obtain:

<br /> \frac{1}{i}\frac{2}{\sqrt{\pi}}\int_0^{-\infty+i\infty} e^{-w^2}dw=\frac{1}{i}\frac{2}{\sqrt{\pi}}(-\frac{\sqrt{\pi}}{2})=-\frac{1}{i}\frac{i}{i}=i<br />

and:

<br /> \frac{1}{i}\frac{2}{\sqrt{\pi}}\int_0^{\infty+i\infty} e^{-w^2}dw=\frac{1}{i}\frac{2}{\sqrt{\pi}}(\frac{\sqrt{\pi}}{2})=\frac{1}{i}\frac{i}{i}=-i<br />

So that the limit is 2i.


Substituting this into the last expression of the inverse transform, we obtain:

<br /> y(x)=\frac{e^{-\pi/t}}{2i t^{3/2}}(2i)=\frac{e^{-\pi/t}}{t^{3/2}}

Thanks for helping me Tide. Couldn't have done this without your help.

 

[Tide]

Way to go, Salty!

 

[saltydog]

So I wish to return to the subject of differential (integral) equations and the numerical evaluation of inverse Laplace Transforms. While going though the analysis above, I realized I can numerically evaluate an integral of a complex variable in the same (similar) way as for a real variable! Take for example the contour expression for the inverse transform:

y(x)=\frac{1}{2\pi i}\int_{1-i\infty}^{1+i\infty}\frac{e^{st}}{e^{2\sqrt{\pi s}}} ds

For the moment, let's consider the case of t=1. In that case, this integral is EXACTLY equal to:

y(1)=e^{-\pi}\approx 0.0432139

Now, for starters, suppose I just calculate a ROUGH Reimann sum for this integral:

\frac{1}{2\pi i}\sum_1^{1000} \frac{e^{st}}{e^{2\sqrt{\pi s}}}\Delta c

along the straight-line contour from the points 1-10i to 1+10i.

This is my Mathematica code:

sum = 0;
tval = 1;
imax = 10;
cval = 1 - i max;
nmax = 1000;
deltai = 2 imax/nmax i;
For[n = 1, n <= nmax, n++,
  cval += deltai;
[tex]sum+=N\left[\left(\frac{e^{\text{cval tval}}}{e^{2\sqrt{\pi\text{cval}}}}\right) \text{deltai}\left][/tex]
];
[tex]sum=\frac{1}{2\pi i} sum[/tex]

The results are:

0.0434844+1.31273X10^{-6} i

Granted there is a slight complex component but the real part agrees with the actual value to 3 decimal places and this is only a rough estimate.

My suspicion is that this will be the case ONLY for alpha=1/2 and that any other value of alpha in the original integral equation will result in a significant complex part meaning that the only REAL solution to the integral equation is the one with alpha=1/2.

Anyone have any thoughts about this?

Tide, you still with me?

 

[Tide]

If real solutions exist to the original integral equation and if the Laplace transforms exist then the inversion must lead to a real result. A numerical approximation may lead to an imaginary part but there are two issues with a numerical approximation: (a) finite step size and (b) infinite domain. It may take that entire "trip" to infinity to eliminate the small imaginary part but it will not be there in the end! :)

 

[saltydog]

Numerical calculations

Hey Tide, I find the following results very encouraging: The first plot is the solution of the integral equation:

y(t)=\frac{e^{-\pi/t}}{t^{3/2}}

The second plot is a numerical evaluation of the inverse transform using a simple Riemann sum over the path 1-20i to 1+20i[/tex] sampling 1000 points. <br /> <br /> The third plot is a superposition of the two. Not bad for a rough approximation.<img src="https://cdn.jsdelivr.net/joypixels/assets/8.0/png/unicode/64/1f642.png" class="smilie smilie--emoji" loading="lazy" width="64" height="64" alt=":smile:" title="Smile :smile:" data-smilie="1"data-shortname=":smile:" /><br /> <br /> Edit: I neglected the &quot;small&quot; residual imaginary component of the numerical calculations.

 

[Tide]

That's pretty good!

If you want to take it a little further, you could do some asymptotic analysis on the integral. When t is large, most of the contribution to the integral (say your first eq. in #11) is from the region about a "saddle point" (e.g. \int e^{\phi(s, t)} ds) has such a point where d \phi(s, t) /ds = 0 and you integrate along the path of steepest descent through the saddle point.

In principle, the asymptotic expansion of the integral will overlap your numerical evaluation over some range of large t values. I haven't looked but you should be able to find a lot of references to the "method of steepest descent" for details.

 

[saltydog]

Thanks Tide. I'll check that out. Here are the plots for alpha =0.5 to alpha=0.1 with the largest one being alpha=0.1, then 0.2, 0.3, 0.4, and the smallest, 0.5.

I've yet to show that these other plots satisfy the integral equation however and plan to work on a back-substitution method to check them (within some level of accuracy).

I'm sure other numerical methods exists for evaluating integral equations, however, to pursue such would have denied me the privilege (and learning experience) of working on this very interesting approach with Laplace Transforms.

 

[saltydog]

I perfected a method of back-substitution of the numeric data into the integral equation in an effort to numerically check the solution for alpha=0.1. The inverse transform is:

y(t)=\frac{1}{2\pi i}\mathop\lim\limits_{a\to\infty}\int_{1-ai}^{1+ai} e^{zt}\text{Exp}\left[-\frac{\Gamma[0.1]}{1-0.1}z^{1-0.1}\right]dz

This can be numerically integrated directly until the results reach a desired level of accuracy. The integral then is evaluated for a range of t. The results of these calculations is shown in plot 1. Mathematica has a nice feature which can represents the data points as a "Interpolation function":

\text{alpha01 = Interpolation[pointlist]}

alpha01 is now treated as a function.

The next step is to numerically evaluate the RHS of the original integral equation:

\int_0^t \tau^{\alpha-1}\text{alpha01}(t-\tau)d\tau

or:

rhs[t]=\int_0^t (t-z)^{\alpha-1}\text{alpha01}(z)dz

The LHS of the integral equation is:

lhs[t]=\text{alpha01[t]t}

Subtracting:

\text{dif[t]=lhs[t]-rhs[t]}

The results of this difference is shown in the second plot showing that the difference is no larger than 10^-6.

This then gives me some confidence that the numerical results for alpha=0.1 do indeed satisfy the integral equation.

 

[saltydog]

For the record I wish to correct a statement I made above:

The integrand has a branch point (singularity) at the origin (caused by the square root of z). Pretty sure anyway. Anyone reading this thread, please forgive my unfamiliarity with the subject. This is all very new for me.
With this in mind, I'd like to evaluate the inverse transform using Cauchy's theorem:

\oint_c \frac{e^{zt}}{e^{2\sqrt{\pi z}}}dz=0

along the contour shown in the first plot below. The second plot is an expanded view of the center contour from D to E. You guys mind if I continue working on this here even though the contour integration is not "directly" relevant to differential equations? The integrals are tough to evaluate and I'll likely need help with them. I've already done some preliminary numerical calculations with all 5 integrals and the results do indeed tend to the desired result.

 

[saltydog]

Before I begin evaluating this contour integral I'd like to justify the path with my limited understanding of the subject:

I need to avoid going through the singularity of a branch cut created by the z^{1/2} term (don't quite understand this part). This cut can be anywhere in the complex plane. Since the definition of the inverse transform requires the path of integration to be right of any singularities, for simplicity I define the cut to be the negative x-axis. Thus to make a closed contour, we go around both the branch cut and the branch point at the origin, hense the keyhole contour. For those unfamiliar with the subject, the actual integration paths are infinitessimally close to both the negative x-axis and the origin. We simply expand the path in the contour diagram so that we can more easily visualize it.

Since the branch cut is at the polar coordinate \theta=\pi, in any integrations involving polar coordinates, we must not go through the value \theta=\pi. Thus in the calculations of the integrals, theta will take on values between 0 and pi and between -pi and pi.

In order to facillitate the evaluation of the inverse transform, we allow the diameter (R in the diagram) of the contour to approach infinity and evaluate the integral at that limit.

Thus, using Cauchy's Integral Theorem and the contour defined above, I integrate along a counter-clockwise direction and arrive at the following expression:

<br /> \begin{align*}<br /> \oint_c f(z)dz&amp;=\int_{AB} f(z)dz+\int_{BC} f(z)dz+\int_{CD} f(z)dz\\<br /> &amp;+ \int_{DE} f(z)dz+\int_{EF} f(z)dz+\int_{FA} f(z)dz=0<br /> \end{align}<br />

Note however at the limit R\to\infty, that

\int_{AB} f(z)dz=\int_{\gamma-i\infty}^{\gamma+i\infty} f(z)dz

This is in fact the integral component of the transform. Thus I can write:

<br /> \begin{align*}<br /> \int_{\gamma-i\infty}^{\gamma+i\infty} f(z)dz&amp;=-\left(\int_{BC} f(z)dz+\int_{CD} f(z)dz+\int_{DE} f(z)dz\right \\<br /> &amp;+\left\int_{EF} f(z)dz+\int_{FA} f(z)dz\right)<br /> \end{align}<br />

Multiplying both sides by \frac{1}{2\pi i}, the inverse transform can be expressed as:

<br /> \begin{align*}<br /> \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty} f(z)dz&amp;=-\frac{1}{2\pi i}\left(\int_{BC} f(z)dz+\int_{CD} f(z)dz+\int_{DE}<br /> f(z)dz\right \\<br /> &amp;+ \left\int_{EF} f(z)dz+\int_{FA} f(z)dz\right)<br /> \end{align}<br />

 

[saltydog]

Letting z=Re^{i\theta} for the first and fourth integral, I obtain:

\int_{BC}=\mathop\lim\limits_{R\to\infty}\int_{\pi/2}^{\pi}\frac{e^{tRe^{i\theta}}}{Exp[2\sqrt{R\pi}e^{i\theta/2}]} iRe^{i\theta}d\theta

\int_{FA}=\mathop\lim\limits_{R\to\infty}\int_{-\pi}^{-\pi/2}\frac{e^{tRe^{i\theta}}}{Exp[2\sqrt{R\pi}e^{i\theta/2}]} iRe^{i\theta}d\theta

For the center contour, let \phi go from \pi to-\pi and let the modulus be \epsilon. Thus letting:

z=\epsilon e^{\phi i}

\int_{DE}=\mathop\lim\limits_{\epsilon\to 0}\int_{\pi}^{-\pi} \frac{e^{t\epsilon e^{i\phi}}}{Exp[2\sqrt{\pi\epsilon}e^{\phi i/2}]}\epsilon i e^{\phi i}d\phi

For the two straight-line segements, I'll use a common (apparently) substituion in complex integration:

For the path C to D, let:

z=-u=ue^{\pi i}

For the path E to F, let:

z=-u=ue^{-\pi i}

Making these substitutions I obtain:

\int_{CD}=\mathop\lim\limits_{R\to\infty,\epsilon\to 0}\int_R^{\epsilon}\frac{e^{-tu}}{e^{2\sqrt{\pi}i\sqrt{u}}} (-du}

\int_{EF}=\mathop\lim\limits_{R\to\infty,\epsilon\to 0}\int_{\epsilon}^{R}\frac{e^{-tu}}{e^{-2\sqrt{\pi}i\sqrt{u}}} (-du}

Putting this all together, I obtain for the inverse transform:

<br /> \begin{align*}<br /> \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+\infty}\frac{e^{zt}}{e^{2\sqrt{\pi z}}} dz&amp;=<br /> -\frac{1}{2\pi i}\left(\mathop\lim\limits_{R\to\infty}\int_{\pi/2}^{\pi}\frac{e^{tRe^{i\theta}}}{Exp[2\sqrt{R\pi}e^{i\theta/2}]} iRe^{i\theta}d\theta \right\\ \\<br /> &amp;+\mathop\lim\limits_{R\to\infty}\int_{-\pi}^{-\pi/2}\frac{e^{tRe^{i\theta}}}{Exp[2\sqrt{R\pi}e^{i\theta/2}]} iRe^{i\theta}d\theta \\ \\<br /> <br /> &amp;+\mathop\lim\limits_{\epsilon\to 0}\int_{\pi}^{-\pi} \frac{e^{t\epsilon e^{i\phi}}}{Exp[2\sqrt{\pi\epsilon}e^{\phi i/2}]}\epsilon i e^{\phi i}d\phi \\ \\<br /> <br /> &amp;+\mathop\lim\limits_{R\to\infty,\epsilon\to 0}\int_R^{\epsilon}\frac{e^{-tu}}{e^{2\sqrt{\pi}i\sqrt{u}}} (-du) \\ \\<br /> <br /> &amp;+\left\mathop\lim\limits_{R\to\infty,\epsilon\to 0}\int_{\epsilon}^{R}\frac{e^{-tu}}{e^{-2\sqrt{\pi}i\sqrt{u}}}(-du)\right)<br /> <br /> <br /> \end{align}<br />

Alright, so I know the first, second, and third go to zero but can't show that for the first and second (not sure about third), and the sum of the fourth and fifth go to the desired result and can kinda' get close to showing that. May take a while . . . can I use the HW section if I need help?

Edit: Oh yea, I realize I'm bitting off more than I can chew with this. It's only a goal I wish to strive for; I'm currently working on simpler ones: Schaum's is a start.

 

[saltydog]

Since I'm unable to evaluate the limits of the first two in terms of \theta, I'll rely on the analyticity of the integrand in the region of integration and it's indepenence of path.

So I'll leave them as:

\int_{BC} \frac{e^{zt}}{e^{\sqrt{\pi z}}}dz

\int_{FA} \frac{e^{zt}}{e^{\sqrt{\pi z}}}dz

and solve for an antiderivative exactly as I did above to obtain:

\int_{BC} \frac{e^{zt}}{e^{\sqrt{\pi <br /> <br /> z}}}dz=\frac{2e^{-\pi/t}}{t}\mathop\lim\limits_{R\to\infty}\int_{\sqrt{Rt}e^{\pi <br /> <br /> i/4}}^{\sqrt{Rt}e^{\pi i/2}} e^{(v-\pi/t)^2}vdt

and:

\int_{FA} \frac{e^{zt}}{e^{\sqrt{\pi <br /> <br /> z}}}dz=\frac{2e^{-\pi/t}}{t}\mathop\lim\limits_{R\to\infty}\int_{\sqrt{Rt}e^{-\pi <br /> <br /> i/2}}^{\sqrt{Rt}e^{-\pi i/4}} e^{(v-\pi/t)^2}vdt

The two integrals in z thus reduce to the same expression above (with different limits):

\int_{BC} f(z)dz=\frac{2e^{-\pi/t}}{t}\left[\mathop\lim\limits_{R\to\infty}\left(e^{(v-\sqrt{\pi/t})^2}+\frac{\pi}{t^{1/2}}\text{Erf<br /> <br /> i}[v-\sqrt{\pi/t}]\right)_{\sqrt{Rt}e^{\pi i/4}}^{\sqrt{Rt}e^{\pi <br /> <br /> i/2}}\right]

\int_{FA} f(z)dz=\frac{2e^{-\pi/t}}{t}\left[\mathop\lim\limits_{R\to\infty}\left(e^{(v-\sqrt{\pi/t})^2}+\frac{\pi}{t^{1/2}}\text{Erf<br /> <br /> i}[v-\sqrt{\pi/t}]\right)_{\sqrt{Rt}e^{-\pi i/2}}^{\sqrt{Rt}e^{-\pi <br /> <br /> i/4}}\right]

Using the same analysis as above, these limits can be shown to approach zero.

Thus I can reduce the expression of the inverse transform to:

<br /> \begin{align*}<br /> \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+\infty}\frac{e^{zt}}{e^{2\sqrt{\pi z}}} dz&amp;=<br /> -\frac{1}{2\pi i}\left(\mathop\lim\limits_{\epsilon\to 0}\int_{\pi}^{-\pi} \frac{e^{t\epsilon e^{i\phi}}}{Exp[2\sqrt{\pi\epsilon}e^{\phi i/2}]}\epsilon i e^{\phi i}d\phi \\ \\<br /> &amp;+\mathop\lim\limits_{R\to\infty,\epsilon\to 0}\int_R^{\epsilon}\frac{e^{-tu}}{e^{2\sqrt{\pi}i\sqrt{u}}} (-du) \\ \\<br /> &amp;+\left\mathop\lim\limits_{R\to\infty,\epsilon\to 0}\int_{\epsilon}^{R}\frac{e^{-tu}}{e^{-2\sqrt{\pi}i\sqrt{u}}}(-du)\right)<br /> \end{align}<br />

 

[saltydog]

The third integral of the inversion is zero by inspection. More interestingly, is to show the following relation:

<br /> -\frac{1}{2\pi i}\left(\int_0^{\infty}\frac{e^{-tu}}{e^{2\sqrt{\pi}i\sqrt{u}}}du-\int_{0}^{\infty}\frac{e^{-tu}}{e^{-2\sqrt{\pi}i\sqrt{u}}}du\right)=\frac{e^{-\pi/t}}{t^{3/2}}

Completing the square of both integrals and using the same substitutions as above:

\sigma^2=u;\quad v=\sqrt{t}\sigma

I obtain:

\int_0^{\infty}\frac{e^{-tu}}{e^{2\sqrt{\pi}i\sqrt{u}}}du=\frac{2 e^{-\pi/t}}t}\int_0^{\infty}e^{-(v+i\sqrt{\pi/t})^2}vdv

\int_{0}^{\infty}\frac{e^{-tu}}{e^{-2\sqrt{\pi}i\sqrt{u}}}du=\frac{2 e^{-\pi/t}}t}\int_0^{\infty}e^{-(v-i\sqrt{\pi/t})^2}vdv

Evaluating both of these integrals:

\frac{2 e^{-\pi/t}}{t}\int_0^{\infty}e^{-(v+i\sqrt{\pi/t})^2}vdv=\frac{e^{-\pi/t}}{t}\left(-\frac{\pi i}{t^{1/2}}+e^{\pi/t}-\frac{\pi}{\sqrt{t}}\text{Erfi}(\sqrt{\pi/t})\right)

\frac{2 e^{-\pi/t}}{t}\int_0^{\infty}e^{-(v-i\sqrt{\pi/t})^2}vdv=\frac{e^{-\pi/t}}{t}\left(\frac{\pi i}{t^{1/2}}+e^{\pi/t}-\frac{\pi}{\sqrt{t}}\text{Erfi}(\sqrt{\pi/t})\right)

Finally, substituting these into the expression for the inverse transform:

<br /> \begin{align*}<br /> \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty}\frac{e^{zt}}{e^{2\sqrt{\pi z}}}dz &amp;=<br /> -\frac{1}{2 \pi i}\left\{\frac{e^{-\pi/t}}{t}\left(-\frac{\pi i}{t^{1/2}}+e^{\pi/t}-\frac{\pi}{\sqrt{t}}\text{Erfi}(\sqrt{\pi/t})\right)\right \\ \\<br /> <br /> &amp;-\frac{e^{-\pi/t}}{t}\left(\left \frac{\pi i}{t^{1/2}}+e^{\pi/t}-\frac{\pi}{\sqrt{t}}\text{Erfi}(\sqrt{\pi/t})\right)\right\} \\ \\<br /> &amp;=\frac{e^{-\pi/t}}{t^{3/2}}<br /> \end{align}<br />

Ok, I'm done.

 

[Tide]

Whew! Now, on to Mellin transforms ...! ;)