- #1
missavvy
- 82
- 0
Hey guys! I just have a question regarding some notes I've been looking at and trying to understand...
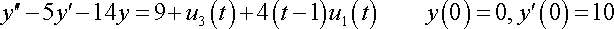
Taking the transform:
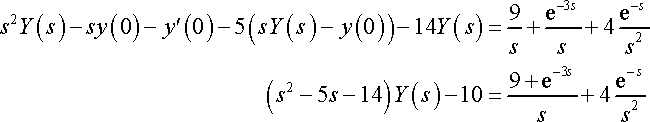
Just wondering, can someone explain to me why the e-3s/s is positive, and not negative because it is originally -u3(t)...
Another quick one:
Write this in terms of Heaviside function:
f(t) =
{ 0, 0 <= t <= pi
{ -sin3t, t >= pi
1) So you would get f(t) = -(upit)sin3t
And somehow it ends up as f(t) = (upit)sin(3(t-pi))
Can someone explain this step as well? Just what happened to the negative in front of it, and why it became 3(t-pi)
Thanks!
Homework Statement
Taking the transform:
Just wondering, can someone explain to me why the e-3s/s is positive, and not negative because it is originally -u3(t)...
Another quick one:
Write this in terms of Heaviside function:
f(t) =
{ 0, 0 <= t <= pi
{ -sin3t, t >= pi
1) So you would get f(t) = -(upit)sin3t
And somehow it ends up as f(t) = (upit)sin(3(t-pi))
Can someone explain this step as well? Just what happened to the negative in front of it, and why it became 3(t-pi)
Thanks!