Laplace Transforms Homework: Initial Displacements & Velocities

[Ray Vickson]

Homework Statement

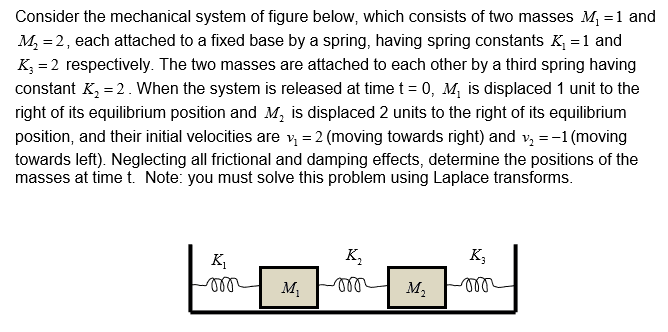
Homework Equations

Laplace Transforms

The Attempt at a Solution

Using basic physics knowledge I got
m₁a₁=-k₁x₁+k₂(x₂-x₁)
and
m₂a₂=-k₃x₂-k₂(x₂-x₁)

Sub in values and use laplace transforms and rearrange partial fraction and I found that

By doing this I am assuming that the x^II and x^III will equal 0 when t=0 because this is not stated at all in the question. do you believe this is correct?x₁=-(1/3)cos2t-(2/3)sin2t+(4/3)cost+(8/3)sint
x₂=-(2/3)cos2t+(1/3)sin2t+(8/3)cost-(4/3)sint

Finding the initial displacements by subbing in t=0 for both _{x_1} and _{x_2} comes out with what is written in the question 1 and 2, respectively.

However, when I try to sub t=0 into the differentials of the 2 above equations. I believe I should receive the initial velocities stated in the question. however I do not receive these results.

I receive 4/3 for x₁ and -2/3 for x₂
the difference between these values and the actual values appears to differ once I differentiate the sin2t and it is multiplied by 2

Does anyone know if I should receive the values listed in the question using this methods and have just made a calculation error in my working earlier on, or should I have done something differently.

Also, the next part of the questions asks to use a matrix and eigenvalues/eigenvectors to solve it. any pointers to help me get started

Thanks very much

I'll just give you a hint for the next part. Let $y_1 = x_1$, $y_2 = dx_1/dt$ (velocity of 1), $y_3 =x_2$ and $y_4 = dx_2/dt$ (velocity of 2). Your DE system can be written as
\begin{array}{rcl}dy_1 /dt &amp;=&amp; y_2 \\<br /> dy_2/dt &amp;=&amp; -3 y_1 + 2 y_3 \\<br /> dy_3/dt &amp;=&amp; y_4\\<br /> dy_4/dt &amp;=&amp; y_1 - 2 y_3\end{array}<br />
This can be written as
\frac{d}{dt} \pmatrix{y_1\\y_2\\y_3\\y_4}=<br /> \pmatrix{0&amp;1&amp;0&amp;0\\-3&amp;0&amp;2&amp;0\\0&amp;0&amp;0&amp;1\\1 &amp;0 -2&amp;0} \pmatrix{y_1\\y_2\\y_3\\y_4}
This is of the form $dY/dt = A Y$, where $Y$ is the column vector of $y_i$s and $A$ is the $4 \times 4$ matrix above. The solution is of the form
Y(t) = \exp(A t) Y(0)
You can compute the matrix exponential from the eigenvalues and eigenvectors (at least, if none of the eigenvalues are repeated). Google 'matrix exponential'.

 

[jake96]

I'll just give you a hint for the next part. Let $y_1 = x_1$, $y_2 = dx_1/dt$ (velocity of 1), $y_3 =x_2$ and $y_4 = dx_2/dt$ (velocity of 2). Your DE system can be written as
\begin{array}{rcl}dy_1 /dt &amp;=&amp; y_2 \\<br /> dy_2/dt &amp;=&amp; -3 y_1 + 2 y_3 \\<br /> dy_3/dt &amp;=&amp; y_4\\<br /> dy_4/dt &amp;=&amp; y_1 - 2 y_3\end{array}<br />
This can be written as
\frac{d}{dt} \pmatrix{y_1\\y_2\\y_3\\y_4}=<br /> \pmatrix{0&amp;1&amp;0&amp;0\\-3&amp;0&amp;2&amp;0\\0&amp;0&amp;0&amp;1\\1 &amp;0 -2&amp;0} \pmatrix{y_1\\y_2\\y_3\\y_4}
This is of the form $dY/dt = A Y$, where $Y$ is the column vector of $y_i$s and $A$ is the $4 \times 4$ matrix above. The solution is of the form
Y(t) = \exp(A t) Y(0)
You can compute the matrix exponential from the eigenvalues and eigenvectors (at least, if none of the eigenvalues are repeated). Google 'matrix exponential'.

thanks

 

[jake96]

I'll just give you a hint for the next part. Let $y_1 = x_1$, $y_2 = dx_1/dt$ (velocity of 1), $y_3 =x_2$ and $y_4 = dx_2/dt$ (velocity of 2). Your DE system can be written as
\begin{array}{rcl}dy_1 /dt &amp;=&amp; y_2 \\<br /> dy_2/dt &amp;=&amp; -3 y_1 + 2 y_3 \\<br /> dy_3/dt &amp;=&amp; y_4\\<br /> dy_4/dt &amp;=&amp; y_1 - 2 y_3\end{array}<br />
This can be written as
\frac{d}{dt} \pmatrix{y_1\\y_2\\y_3\\y_4}=<br /> \pmatrix{0&amp;1&amp;0&amp;0\\-3&amp;0&amp;2&amp;0\\0&amp;0&amp;0&amp;1\\1 &amp;0 -2&amp;0} \pmatrix{y_1\\y_2\\y_3\\y_4}
This is of the form $dY/dt = A Y$, where $Y$ is the column vector of $y_i$s and $A$ is the $4 \times 4$ matrix above. The solution is of the form
Y(t) = \exp(A t) Y(0)
You can compute the matrix exponential from the eigenvalues and eigenvectors (at least, if none of the eigenvalues are repeated). Google 'matrix exponential'.

so I got the Eigen values as i, -i, 2i, -2i

for i, i found an Eigen value of
-i
1
-i
1
Does this seem correct?
Now if i find the eigenvectors for the other eigenvalues. i can use this in the exponential equation and eventually reach values of x₁ and x₂ which should be the same answers from the previous part of the question?

 

[jake96]

I am also having trouble finding good sites online that delve into complex eigenvalues and eigenvectors for any matrix above 2x2. My textbook does touch on this and i was just wondering if anyone knew of anywhere good that i can find some examples to refer to.

 

[vela]

so I got the eigenvalues as i, -i, 2i, -2i

for i, i found an eigenvector of
-i
1
-i
1
Does this seem correct?

It's easy enough to check yourself. Multiply it into the matrix and see if you get $i$ times the vector back.

Now if i find the eigenvectors for the other eigenvalues. i can use this in the exponential equation and eventually reach values of x₁ and x₂ which should be the same answers from the previous part of the question?

Yes.

 

[jake96]

So now that I have my eigenvalues and eigenvectors. I believe I now use them for the exponential matrix and that should give me my sin and cos equations of x₁ and x₂ from earlier in the question. However I am unsure how I am able to reach this point as I have not fully learned this yet and am unable to find suitable sources. Does anyone know of a decent source?

 

[Chestermiller]

Are you familiar with $e^{iθ}=cosθ+isinθ$? If the eigenvalues and eigenvectors were real, would you know how to proceed next?

Chet

 

[jake96]

ive only ever used it for 2x2 matrix's, I assume this way I would receive 4 equations with 4 unknowns? I'm still a little unsure as to how those unknowns are calculated, will the 4 equations be equal to the 4 y equations that Ray Vickson listed?

 

[jake96]

also I just want to double check, if I had the eigenvalue of 'i' and the corresponding eigenvector (-i,1,-i,1)
the first term of the first y equation would be -i(acost+ibsint)
with a and b as unknowns
and so on with each value and vector

 

[jake96]

Are you familiar with $e^{iθ}=cosθ+isinθ$? If the eigenvalues and eigenvectors were real, would you know how to proceed next?

Chet

OK, so I believe I have gotten my four y equation out with 4 unknowns c₁, c₂, c₃ and c₄. What will these 4 equations equal so that I am able to determine the value of each 'c'

 

[Ray Vickson]

So now that I have my eigenvalues and eigenvectors. I believe I now use them for the exponential matrix and that should give me my sin and cos equations of x₁ and x₂ from earlier in the question. However I am unsure how I am able to reach this point as I have not fully learned this yet and am unable to find suitable sources. Does anyone know of a decent source?

Check out the concept of "matrix function". Basically, if $f(x) = c_0 + c_1 x + c_2 x^2 + \cdots$ is an analytic function of $x$, we can define $f(A) = c_0 I + c_1 A + c_2 A^2 + \cdots$ for an $n \times n$ matrix $A$. Here, $I = n \times n$ unit matrix. It is a fact that for a matrix with $n$ distinct eigenvalues $\lambda_1, \lambda_2, \ldots, \lambda_n$ we can find $n$ matrices $E_1, E_2, \ldots, E_n$ such that
f(A) = E_1 f(\lambda_1) + E_2 f(\lambda_2) + \cdots + E_n f(\lambda_n)
The crucial point is that the matrices $E_1, E_2, \ldots, E_n$ are independent of the function $f$. That means we can find them by applying this formula successively to the functions $f_0(x) = 1 = x^0, f_1(x) = x, f_2(x) = x^2, \ldots, f_{n-1}(x) = x^{n-1}$ using the known (or computable) matrices $I = A^0, A, A^2, \ldots, A^{n-1}$.

If you have repeated eigenvalues the formula becomes a bit more complicated.

See, eg., http://www.siam.org/books/ot104/OT104HighamChapter1.pdf or
Gantmacher, "Theory of Matrices, Vol. I", Chapter 5; now available free as http://www.maths.ed.ac.uk/~aar/papers/gantmacher1.pdf .

 

[jake96]

thanks for your help everyone, I've managed to get the correct answer using a 2x2 matrix made from the original equations