Let’s assume the base of the pyramid is a tetragon (a 4-sided polygon) having the points A, B, C, & D as its vertices. A tetragon is a 2-dimensional figure and, as such, all points on the edge of, and in the interior of the tetragon are co-planar. Let’s call the plane within which the tetragon lies (the base of the pyramid), plane G.
The pyramid must have as many sides as the base (in this case, four) and the edges between those sides must meet at a single, common point E above the base (not on plane G).
In the interest of clarity, I’ll call an edge between any 2 sides of the pyramid (not including the base) an “edge” and any edge between one side and the base (one side of the tetragon) a “base edge.” Also, I’ll call an edge that connects vertex A to apex E (the top of the pyramid), “edge A” (naming it by the base vertex that it intersects).
You are trying to determine if there exists a pyramid such that each of its four edges is perpendicular to at least one of the base edges.
It should be evident by inspection that there is not such a pyramid. The best that you can do is construct a pyramid such that three of its side edges (you call “lateral edges”) meet your qualification.
Here’s the proof:
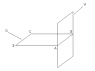
First, let’s consider the edge A. To be perpendicular to a base edge, it must intersect that edge; therefore it can be only be perpendicular to either base edge AD or base edge AB. At this point, we have total symmetry, so it is up to us as to how we should start. I chose AD as the base edge to which the edge A is perpendicular. For this edge to be perpendicular to base edge AD, it must lie within plane W which is perpendicular to plane G intersecting along AB. As to whether the other end of this edge, point E, is above or below plane G (again we have total symmetry), let’s assume it is above. This gives us 5 possibilities as to the position of point E with respect to plane G:
1) Directly above point A (therefore making AE perpendicular to both AB & AD
2) Directly above point B
3) Directly above AB such that it is directly above a point lying between A & B
4) Not above AB such that it is directly above a point on the line containing AB on the side of A opposite of point B
5) Not above AB such that it is directly above a point on the line containing AB on the side of B opposite of point A
Now, let’s consider edge C (having a base vertex diagonally opposite that of edge A). It can be perpendicular to either base edge BC or base edge CD. If we choose that the edge C is perpendicular to CD, then it must lie in plane Y perpendicular to plane G intersecting along CD. But, since AB is parallel to CD, then plane W is parallel to plane Y and the 2 edges cannot intersect. Therefore, we MUST select base edge BC as the perpendicular to edge C. In that case, the edge must lie on plane X which is perpendicular to plane G intersecting along BC. Plane X also intersects plane W along a line perpendicular to plane G through point B.
It is now evident that the only possibility for point E is case #2 above: that it lies directly above point B. This is the only location that allows AE and CE to be perpendicular to some base edge.
Having established a location for point E (but not a distance above plane G), this leaves 2 more edges to identify: Edge BE is perpendicular to base edges AB & BC since it lies on the intersection of planes W & X (and therefore within both planes).
For DE to be perpendicular to a base edge, it must lie in either plane Y or plane Z (which is perpendicular to plane G intersecting along base edge AD). But, the line segment from D to where we determined E to be, does NOT lie within either of those planes and therefore is not perpendicular to a base edge.
On the other hand, the question you may really be asking is whether or not there exists a pyramid such that each of its sides is perpendicular to one of the base edges where the base is any quadrilateral. (I’m still working on that one).