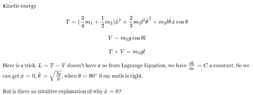When people say "rolling without slipping" they mean that the point on the wheel that is in contact with the surface is instantaneously at rest relative to all points on the surface. In other words, the points that are in contact do not move relative to each other. When there is slipping, the points in contact move relative to each other.
The figure below shows what I am asking you to imagine. In the front view, the stick falls so that its free end moves out of the screen. In the side view, the free end rotates clockwise in the plane of the screen.
View attachment 291923