LC Circuit with DC power supply

[Mola]

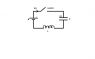
A circuit has a battery(V), Capacitor(C) and Inductor(L) connected in series. At t < 0, the switch is open and the capacitor has an initial charge of -800uC and Io = 0.0Amps.. When the switch is closed at t = 0, I want to know what happens here. I only understand an LC circuit where there is only a capacitor and an inductor, but the addition of a battery in this case makes it a little conplicated for me.



V - Ldi/dt - q(t)/C = 0; q(t)= qmax*cos(wt + phi) + VC; I(t)= -w*qmax*sin(wt + phi).




This is what I think: At t = 0 when the switch is closed, the capacitor starts discharging through the inductor and current increases in the circuit. But the battery is also connected in the circuit, so what is the battery doing? Is it continuosly charging the capacitor? I am confused!

 

[ehild]

Yes, the battery charges the capacitor, meanwhile the changing current induces voltage in the inductor and results in a sinusoidal current and a sinusoidally changing charge superposed to a constant charge on the capacitor.
You have the equation for the circuit.
The solution of this differential equation is the sum of the general solution of the homogeneous equation (with V=0) plus a solution of the inhomogeneous equation (Q=VC), as you have written in your post. You need to substitute the expressions for q(t) and i(t) in the differential equation and in the initial conditions and solve for the unknowns.

ehild

 

[Mola]

Could you please briefly explain your first sentence again? I don't think I get it that well.

But this is what I did:
w = sqrt(1/LC); Period = 2*pi/w; Total energy = (q₀²)/2C + .5*L*I²;
phi = cos^-1(q₀/q_max).

Now I want to find the maximum power storage in the battery during the circuit oscillations and the first time after the switch is closed when the battery reached this maximum power storage.

Will I be right by claiming maximum power storage in batt = V*I_max??

 

[ehild]

Without the battery, both the charge and current would oscillate around zero as the energy of the electric field in the capacitor and the magnetic field energy of the coil periodically transform into each other.
With the battery and without the inductor, the charge would be CV on the capacitor. When you have capacitor, inductor and battery together, the charge oscillates around CV instead of zero, and some of the energy is stored in the battery.

The expressions you got for w and t are correct.

For the total energy, you should be more specific. q and I are interrelated, use the initial conditions q(0)=-800 uC and i(0)=0 to get phi and qmax. Use them to get the energy of both the capacitor and the inductor.

As for maximum power storage in the battery, I am sorry, I do not know what it means.

ehild

 

[Mola]

Ok that was very helpful, thanks. I guess the graph i drew for q vs t is wrong since charge is not oscilatting around zero; but I can fix that.

So about energy transformation:
*Before the switch is closed, at t < 0, the capacitor is fully charged and it has all the energy(in it's electrical field), no energy in inductor, and current = 0.

*When the switch is closed at t = 0, the capacitor starts discharging, current starts increasing, the inductor starts getting some energy and storing it in it's magnetic field.

At some point, the inductor will have all the energy in it's magnetic field and the capacitor will have no charge, and current will be maximum.

Bolded phrases are my questions. Since the battery is also storing some energy, then I cannot claim the capacitor or the inductor will have all the energy at any time. Seems like they have to share the energy with the battery.

Do you know when the battery stores or supplies energy? How are they transfering energy?

 

[ehild]

So about energy transformation:
*Before the switch is closed, at t < 0, the capacitor is fully charged and it has all the energy(in it's electrical field), no energy in inductor, and current = 0.

Right.

*When the switch is closed at t = 0, the capacitor starts discharging, current starts increasing, the inductor starts getting some energy and storing it in it's magnetic field.

At some point, the inductor will have all the energy in it's magnetic field and the capacitor will have no charge, and current will be maximum.

When the current is maximum, the charge is VC on the capacitor.

Bolded phrases are my questions. Since the battery is also storing some energy, then I cannot claim the capacitor or the inductor will have all the energy at any time. Seems like they have to share the energy with the battery.

Do you know when the battery stores or supplies energy? How are they transfering energy?

You are right, part of the energy is stored in the battery.
This is quite an interesting and unusual problem, I never met such one.

Before closing the switch, all the energy is stored in the capacitor. This energy will be conserved in the whole circuit after closing the switch as there are no dissipative elements in the circuit.

If you write out the energy of the capacitor + energy of the inductor at any time, you will see that the expression oscillates between a maximum and minimum value. The difference between this sum and the original energy of the capacitor is supplied/stored by the battery.

A battery always stores energy as chemical energy, it is the product of its emf and the charge it can supply. Here, charge is withdrawn from it and given back periodically, reversing the discharge process. In reality, a battery always has some internal resistance and the chemical processes are not quite reversible: energy will be lost.


ehild