JD_PM
- 1,125
- 156
- TL;DR Summary
- I want to compute the Christoffel-symbol for a given metric.
I am using the code provided by Artes here, but I am missing something.
The Chrisfoffel-symbol formula is
$$\Gamma^{\mu}_{\phantom{\mu}\nu\sigma}=\frac{1}{2}g^{\mu\alpha}\left\{\frac{\partial g_{\alpha\nu}}{\partial x^{\sigma}}+\frac{\partial g_{\alpha\sigma}}{\partial x^{\nu}}-\frac{\partial g_{\nu\sigma}}{\partial x^{\alpha}}\right\}\quad$$
The metric is given to be$$
g_{\mu \nu} =
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & r^2+b^2 & 0 & 0 \\
0 & 0 & (r^2+b^2)\sin^2(\theta) & 0 \\
0 & 0 & 0 & -1
\end{pmatrix}
$$
The provided solution is:
$$\Gamma^{1}_{22}=-r$$
$$\Gamma^{1}_{33}=-r\sin^2(\theta)$$
$$\Gamma^{2}_{21}=\frac{r}{b^2+r^2}$$
$$\Gamma^{2}_{33}=-\cos(\theta)\sin(\theta)$$
$$\Gamma^{3}_{31}=\frac{r}{b^2+r^2}$$
$$\Gamma^{3}_{32}=\cot(\theta)$$
The code I'm using is
But I get
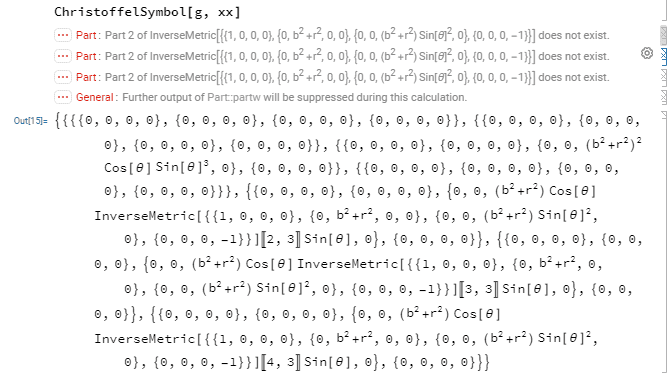
What am I missing? Besides, I'd like to learn how could I display the answer (once I know how to actually get it of course).
Any help is appreciated.
Thank you
The Chrisfoffel-symbol formula is
$$\Gamma^{\mu}_{\phantom{\mu}\nu\sigma}=\frac{1}{2}g^{\mu\alpha}\left\{\frac{\partial g_{\alpha\nu}}{\partial x^{\sigma}}+\frac{\partial g_{\alpha\sigma}}{\partial x^{\nu}}-\frac{\partial g_{\nu\sigma}}{\partial x^{\alpha}}\right\}\quad$$
The metric is given to be$$
g_{\mu \nu} =
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & r^2+b^2 & 0 & 0 \\
0 & 0 & (r^2+b^2)\sin^2(\theta) & 0 \\
0 & 0 & 0 & -1
\end{pmatrix}
$$
The provided solution is:
$$\Gamma^{1}_{22}=-r$$
$$\Gamma^{1}_{33}=-r\sin^2(\theta)$$
$$\Gamma^{2}_{21}=\frac{r}{b^2+r^2}$$
$$\Gamma^{2}_{33}=-\cos(\theta)\sin(\theta)$$
$$\Gamma^{3}_{31}=\frac{r}{b^2+r^2}$$
$$\Gamma^{3}_{32}=\cot(\theta)$$
The code I'm using is
Code:
xx = {t, x, \[Theta], \[Phi]};
g = { {1,0,0,0},
{0,r^2+b^2,0,0},
{0,0,(r^2+b^2)Sin[\[Theta]]^2,0},
{0,0,0,-1}};
ChristoffelSymbol[g_, xx_] :=
Block[{n, ig, res},
n = 4; ig = InverseMetric[ g];
res = Table[(1/2)*Sum[ ig[[i,s]]*(-D[ g[[j,k]], xx[[s]]] +
D[ g[[j,s]], xx[[k]]]
+ D[ g[[s,k]], xx[[j]]]),
{s, 1, n}],
{i, 1, n}, {j, 1, n}, {k, 1, n}];
Simplify[ res]
]But I get
What am I missing? Besides, I'd like to learn how could I display the answer (once I know how to actually get it of course).
Any help is appreciated.
Thank you