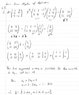Least squares problem - Leon Ch 5, sec.3, prob.3

[IntroAnalysis]

Homework Statement

For the system Ax = b, find least squares solution.

A = (1 2) ; b = (3, 2, 1)^T
----(2 4)
----(1 -2)

Homework Equations

I know if A is an m x n matrix of rank n, the normal equations

A^TAx = A^Tb

have a unique solution x = (A^TA)^-1A^Tb

However, the matrix A is not linearly independent, and is only rank = 1.

Using Gaussian elimination, I think this system of equations is inconsistent. But book gives
answer {(1 - 2α, α)^T; α real}

I don't see how they get this. Aren't these the equations of 3 parallel lines?

 

[lanedance]

isn't A of rank 2?

i would interpret {(1 - 2α, α)T; α real} as a line in R^2

 

[hotvette]

Something is wrong. The problem as stated has a unique solution. The book implies an infinite number of solutions, which isn't true based on the problem statement. Maybe there is a typo in A?

 

[lanedance]

shouldn't the least squares solution to a 2 variable case be a "line of best fit" relating the variables?

 

[IntroAnalysis]

Yes, I believe you are correct. I've attached my work. Also, (A^TA) is singular, so
there isn't an inverse of (A^TA). Of course, the only examples I see in this section of the book are invertible.

Again, anyone know how they come up with their solution {(1 - 2α, α)^T such that α real}?

 

[IntroAnalysis]

No, A isn't a rank of 3. The vectors (2, 4) and (-1, -2) are linear combinations of (1, 2). Hence, rank of A is the one vector (1,2). The nonzero rows of the row echelon matrix form a basis for the row space.

 

[lanedance]

you've written (1,-2) in the original problem

 

[IntroAnalysis]

Darn it, you are correct, I obviously was having problems using Latex for set notation.
Set A should be row 1: 1 2
row 2: 2 4
row 3: -1 -2

and b = (3, 2, 1)^T

Thanks for noticing the typo.

 

[LCKurtz]

Your three equations are

x+2y = 3
2x+4y = 2
-x-2y=1

These equations are inconsistent so they can't all be satisfied. You are looking for (x,y) that minimizes the sum of squares of the errors:

w = (x+2y-3)²+(2x+4y-2)²+(-x-2y-1)²

I would work it as a two variable calculus minimization problem.

 

[hotvette]

Darn it, you are correct, I obviously was having problems using Latex for set notation.
Set A should be row 1: 1 2
row 2: 2 4
row 3: -1 -2

and b = (3, 2, 1)^T

Thanks for noticing the typo.

You also have a typo in your hand written analysis that you posted. Look at your calculation of A^TA. The last row of A has a typo. To answer your question how the book got their answer, you need to look at solving A^TAx = A^Tb. It is singular as you state. This means there is either no solution or an infinite number of them. In this particular case you end up with two identical equations which is the same as one equation with two unknowns. Let one of the unknowns take on an arbitrary value (the book let x₂ = a) and you'll get your answer.

 

[IntroAnalysis]

Correct, (A^TA) should come out to
(6 12)
(12 24)

The determinant = 144 - 144 = 0, so still singular.

If I take the person's advice and take partial derivatives of w w.r.t x and y:

w = (x - 2y - 3)² + (2x + 4Y - 2)² + (-x - 2y - 1)²

I get dw/dx = 12x + 24y - 12 = 12(x + 2y -1) = 0
dw/dy = 24x + 48y - 24 = 24(x + 2y -1) = 0

letting y = α, then x = 1 - 2α and the solution {(1 - 2α), α; for all α element of Real}

This looks like the long way to get at what N(A^T) looks like.

 

[IntroAnalysis]

I saw my professor about this problem yesterday. While the method suggested here works, it is not the best way to solve this problem.

See attached. But we know that : (A^TA)x = A^Tb is always consistent.

So we can solve reducing it with Row Echelon Form. This is the most efficient way to solve this problem.

I was relying on following the examples from this section too much. My professor had said (when showing how cumbersome finding an inverse matrix can be), "No one solves them like this." I thought he meant they use computers or calculators. That is where I got confused.