Let A={(x,y):x>0,x^2>y>0}. Prove for all lines through (0,0)

[Eclair_de_XII]

Homework Statement

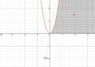
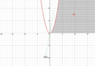
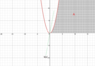
"Let $A=\{(x,y)\in ℝ^2: x>0,\space x^2 > y > 0\}$. Prove that for all lines $b(x)=\langle x,ax \rangle,\space a,x\in ℝ$ passing through $(x,y)=(0,0)$, there exists an interval along that line $b(x)$ that is not in $A$."

Homework Equations

Ball of radius $\epsilon$ centered around $(a,b)$: $B((a,b),\epsilon)$
Set of points intersected by a line $l(x)$ with length $|t|⋅|l(x)|$: $\{t⋅l(x):t\in ℝ\}$

The Attempt at a Solution

Basically, I constructed an interval of $b(x)$, with $|b(x)|=1$ centered about $(x,y)=(0,0)$ by forming the intersection: $B((0,0),\epsilon)\cap \{tb(x):t\in ℝ\}=\{|t|<\epsilon\}$.

I was going to show that if $t\in (-\epsilon,\epsilon)\cap \{t:xt<0\}\subset \{|t|<\epsilon\}$, that $\{tb(x)\}⊄A$, but couldn't figure out how to express it. I'm not completely sure that the rough solution is correct, either. For one, the set falls apart whenever $x=0$. And this is basically the sketch of what I'm working with, here.

There's also a part two to this problem, but I think I should hold back on that until I've finished part one.

 

[andrewkirk]

First consider the easy cases:

1. a<0.
2. a=0

For those cases you should be able to prove that the entire line lies outside A.

The remaining case is where a>0. Looking st the diagram, it's clear that it will be the part of the line in the first quadrant that is closest to the origin, that will be outside a. In particular it will be above A. Try to write an inequality involving $x$ that is satisfied iff the point $(x,ax)$ is outside A. You'll get a quadratic inequality. From that you should be able to deduce over what set of values of $x$ the inequality holds, and thereby show that the set contains an open interval. .

 

[Eclair_de_XII]

Thanks for the pointers; it really simplified how to approach the solution. Anyway, so I should be done with part 1. Here's part 2 and my attempt.

1. Homework Statement
"Define $F:ℝ^2 \rightarrow ℝ$ by $f(x)=0$ if $x\notin A$ and $f(x)=1$ if $x\in A$. For $h\in ℝ^2$, define $g_h:ℝ\rightarrow ℝ$ by $g_h(t)=f(th)$. Show that each $g_h$ is continuous at $0$, but $f$ is not continuous at $(0,0)$."

Homework Equations

The Attempt at a Solution

(1)
First, I want to prove that $g_h$ is continuous at $0$ (which I assume to is supposed to mean at $t=0$. So I wanted to do an epsilon/delta argument, but got stuck. Basically, I have the inequality: $|t(x,y)-(0,0)|=|t⋅(x,y)|=|t|⋅|(x,y)|=0<\delta$. But I don't know how to draw an implication that $|g_h(t)-0|<\epsilon$ follows from $\delta >0$

(2)
As for showing that $f$ is not continuous at $(0,0)$, I had planned on setting $\delta>0$. Then I was going to show that $B((0,0),\delta)$ contains points from both $A$ and $A^c$. I was going to do a proof by contradiction for this part. I let $\epsilon = \frac{1}{2}$. Then I assumed that to the contrary that if $x\in B((0,0),\delta)$ then that implied that $|f(x)-1|<\frac{1}{2}$ and $|f(x)-0|<\frac{1}{2}$. After, I had planned on using the triangle inequality to show that contradiction.

I haven't actually written down this solution yet; this is just a rough draft of what I would do with my current knowledge.

 

[Eclair_de_XII]

Okay, I figured it out by looking at my notes. According to my notes, part 1 of the second part should be clear from the work done on the first.

Thanks for your help, @andrewkirk.