chwala said:
small error you meant denominator not numerator...
Correct. Sorry.
Now, what about his Taylor series approach ? As you see from the
description, it's a way to write a function as a polynomial where the derivatives appear in the coefficients. So instead of differentiating numerator and denominator until one of the two is nonzero in the limit, you look at these coefficients.
Note: I don't think I ever heard of l'Hôpital until I started to 'work' for PF.
In the toolkit of nearly all scientists there is the first (or sometimes a few) of these
Taylor coefficients for frequently occurring functions. They are extremely useful for estimating behaviour af composite functions, for taking limits, for estimation, numerical procedures etc, etc. In this exercise we need
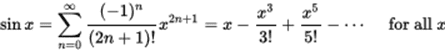
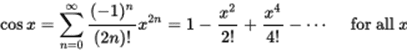
(pictures from Wikipedia - having a hard time letting them appear as pictures)
I had to look them up, for a reason:
'Everyone' knows that 'sine goes like x' and that 'cosine goes like ##\ 1-x^2/2\ ## for small x. But your slightly sadistic exercise composer carefully concocted a quotient that goes to zero like ##\ {ax^4\over b x^4}\ ##.
In the denominator you see a ##\ 2x^4\ ## as the first nonzero term in the Taylor series. So in this exercise the denominator goes like ##\ 16 x^4 \ ##And that's all you need to know for this exercise (that sure beats differentiating four times and derailing once or twice on the way, doesn't it ?). If the numerator goes like 'x to the less than four' the limit doesn't exist and for 'x to the more than four' the limit is zero.
And in the numerator some work is required, for the first coefficients are 'coincidentally' canceling: 9-8+1 . And so is the next coefficient (for ##\ x^2\ : \ 9 * {1\over 2} - {1\over 2} * 9 \ ##) so we need terms up to ##x^4## (of course -- look at the denominator).
And even lazy me was curious enough to work on $$ - 9\left (1-{x^2\over 2} + {x^4\over 24}\right ) + \left (1-{(3x)^2\over 2} + {(3x)^4\over 24}\right )$$ until I had ##\ {72\over 24 }\ ##. (That's why I expected 384 = 16 * 24 in your final denominator fourth derivative). Granted, it's work, but a lot less work than differentiating four times and derailing once or twice on the way.
- - - -
So much for the lecture notes. I called this a quasi-alternative approach because you still work with the derivatives that are tucked away in the coefficients of the Taylor series.
@ehild came (#41) with the suggestion to express numerator and denominator as polynomials of cosines. I still see a lot of work coming at me to then do l'Hôpital but perhaps she saw a shorter path through ?

 )
)