I How Does the Limit of cosh and sinh Approach 1?

[thegirl]

Hi I was wondering how you get this when taking the limit of T going to 0

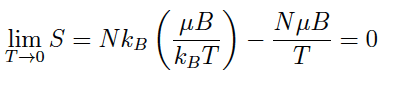
From this expression of S:

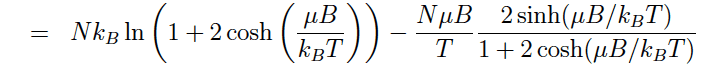
Please help I don't see how ln infinity goes to uB/KbT (used u to represent the greek letter. And how does the other expression of sinh and cosh approach 1?

 

[phyzguy]

Both sinh(x) and cosh(x) approach e^x as x->infinity. Do you see why? So the 1 term becomes negligible compared to the cosh term. Does this help?

 

[thegirl]

Both sinh(x) and cosh(x) approach e^x as x->infinity. Do you see why? So the 1 term becomes negligible compared to the cosh term. Does this help?

is that because when x aproaches infinity cosh(x) = infinity and as e^x also approaches infinity when x approaches infinity it can be said that lim(x-> infinity) cosh(x) = (lim x-> infinity)e^x? Also, thanks for replying!

 

[Ssnow]

As $T\rightarrow 0$ we have that $\ln{\left(1+2\cosh{\left(\frac{\mu B}{k_{B}T}\right)}\right)}\sim \ln{\left(1+ e^{\left(\frac{\mu B}{k_{B}T}\right)}\right)}\sim \frac{\mu B}{k_{B}T}$ ...

 

[phyzguy]

is that because when x aproaches infinity cosh(x) = infinity and as e^x also approaches infinity when x approaches infinity it can be said that lim(x-> infinity) cosh(x) = (lim x-> infinity)e^x? Also, thanks for replying!

cosh(x) = \frac{e^x + e^{-x}}{2}

As x->infinity the e^(-x) term approaches zero and becomes negligible compared to the e^x term.