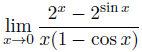MHB How can I solve this limit without using L'Hôpital's rule?

[goody1]

I need to solve this limit without L'Hôpital's rule. Could someone give me a hint what
I need to do please? I just can't find this algebraic trick. Thank you in advance!

 

[topsquark]

One of the usual ways to get around l'Hopital is to use series representations (which I personally think is cheating.) But this one's a monster to do this way.
[math]2^x \approx 1 + (x ~ ln(2) ) + \dfrac{1}{2} (x ~ ln(2) )^2 + \dfrac{1}{6} (x ~ ln(2) )^3 + \text{ ...}[/math]

[math]2^{sin(x)} \approx 1 + (x ~ ln(2) ) + \dfrac{1}{2} (x ~ ln(2) )^2 + \dfrac{1}{6} x^3 ( (ln(2)^3 - ln(2) ) + \text{ ...}[/math]

[math]cos(x) \approx 1 - \dfrac{1}{2} x^2 + \text{ ...}[/math]
(These are MacLaurin series.)

So
[math]\dfrac{ 2^x - 2^{sin(x)} }{x (1 - cos(x) ) } \approx \dfrac{ \dfrac{1}{6} x^3 ln(2) }{x \left ( 1 - \left ( 1 - \dfrac{1}{2} x^2 \right ) \right ) } = \dfrac{1}{3} ln(2)[/math]

Ugly, but doable. (And yes, I did the [math]2^{sin(x)}[/math] series myself. I only checked it with W|A.)

-Dan

 

[goody1]

Thank you for showing me this solution, it looks pretty elegant! But do you think there is other possible way how to solve it? The problem is we've never learned this method so I think I can't use it on my exam when we'll have to solve similar trigonometric limit.