Limits and Continuity - Absolute Value Technicality ....

Click For Summary
SUMMARY

The discussion centers on proving an inequality involving absolute values as presented in Example 4.1.2 (a) from Manfred Stoll's "Introduction to Real Analysis." The key statement is that if \( |x - p| < 1 \), then it follows that \( |x| < |p| + 1 \). Peter effectively demonstrates this using the triangle inequality, establishing that \( |x| - |p| \leq |x - p| < 1 \), leading to the conclusion that \( |x| < 1 + |p| \). This proof highlights the application of fundamental concepts in real analysis.

PREREQUISITES
  • Understanding of absolute value properties
  • Familiarity with the triangle inequality
  • Basic knowledge of limits and continuity in real analysis
  • Experience with mathematical proofs and inequalities
NEXT STEPS
  • Study the triangle inequality in depth
  • Explore more examples in "Introduction to Real Analysis" by Manfred Stoll
  • Learn about rigorous proof techniques in real analysis
  • Investigate the implications of limits and continuity on inequalities
USEFUL FOR

Students of real analysis, mathematics educators, and anyone seeking to deepen their understanding of limits, continuity, and absolute value inequalities.

Math Amateur
Gold Member
MHB
Messages
3,920
Reaction score
48
I am reading Manfred Stoll's Book: "Introduction to Real Analysis" ... and am currently focused on Chapteer 4: Limits and Continuity ...

I need some help with an inequality involving absolute values in Example 4.1.2 (a) ...

Example 4.1.2 (a) ... reads as follows:

?temp_hash=3b7c8f68814a2778b219da7337e2fc04.png
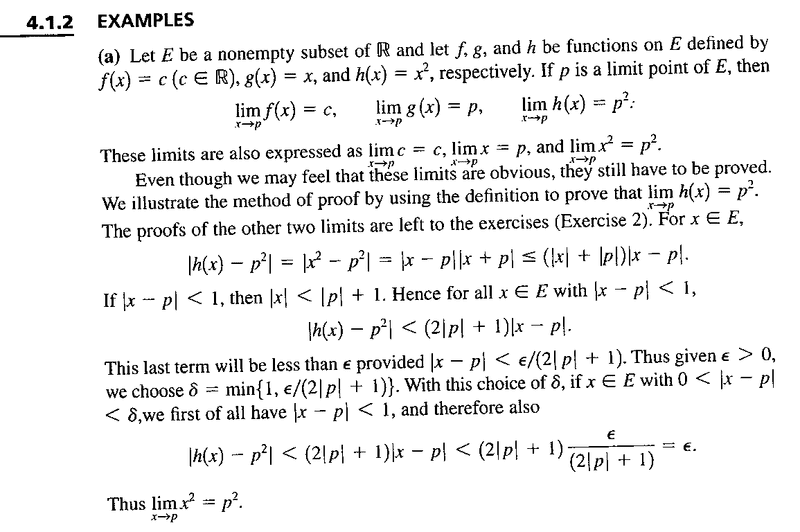In the above text we read ...

"... If ## \mid x - p \lvert \ \lt 1## then ##\mid x \mid \lt \mid p \mid + 1 ## ... "Can someone please show me how to rigorously prove the above statement ...

Peter
 

Attachments

  • Stoll - Example 4.1.2 (a).png
    Stoll - Example 4.1.2 (a).png
    39.7 KB · Views: 949
Physics news on Phys.org
Just use the triangle inequality.
 
  • Like
Likes   Reactions: Math Amateur
##|x| = |x-p+p| \leq |x-p| + |p| \Rightarrow |x| - |p| \leq |x-p| < 1 \Rightarrow |x| < 1 + |p|##
 
  • Like
Likes   Reactions: Math Amateur

Similar threads

MHB Limits and Continuity - Absolute Value Technicality ....
  • · Replies 3 ·
Replies
3
Views
1K
MHB Intermediate Value Theorem .... Browder, Theorem 3.16 .... ....
  • · Replies 2 ·
Replies
2
Views
3K
Undergrad Intermediate Value Theorem .... Browder, Theorem 3.16 .... ....
  • · Replies 4 ·
Replies
4
Views
2K
MHB The Euclidean Norm is Lipschitz Continuous .... D&K Example 1.3.5 .... ....
  • · Replies 2 ·
Replies
2
Views
3K
MHB Convergence of Geometric Series .... Sohrab, Proposition 2.3.8 .... ....
  • · Replies 2 ·
Replies
2
Views
2K
MHB Linear Mappings are Lipschitz Continuous .... D&K Example 1.8.14 .... ....
  • · Replies 2 ·
Replies
2
Views
2K
MHB Law of Cosines for C .... Remmert Section 1.3, Ch. 0 ....
  • · Replies 1 ·
Replies
1
Views
1K
MHB Heine-Borel Theorem & D&K Theorem 1.8.17 | Peter's Question
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Bounded in Norm .... Garling, Section 11.2: Normed Spaces ....
  • · Replies 2 ·
Replies
2
Views
3K
MHB Bounded in Norm .... Garling, Section 11.2: Normed Spaces ....
  • · Replies 5 ·
Replies
5
Views
2K