- #1
Nicolas Gallardo
- 12
- 0
Homework Statement
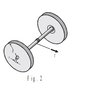
The object of the figure below has 2 disks attached on both sides through and axel of negligible mass. Both disks of mass M. I need to find the linear acceleration of this object knowing there exists a tension T on the cord.
Homework Equations
:[/B]T=αI
The Attempt at a Solution
:[/B]First we know that :
τ=αI ⇒
T(R-r)=I(a/R)⇒
T(R-r)=(2(MR^2)/2)(a/R)⇒
T(R-r)=MRa⇒
a=(T(R-r))/(MR)
But the solution of the exercise is : a=(T(R-r))/(3MR)
What am I doing wrong?
Attachments
Last edited: