Linear Applications: Electrical Networks

[Pull and Twist]

So I am having difficulty with the following problem;

Determine the currents in the various branches.

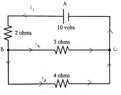
View attachment 5184

So I went ahead and assigned I names to the various branches and drew in flow directions to help me visualize the problem better.

From there I created the following three equations;

I₁=I₂+I₃
2I₁+3I₂=10
2I₁+4I₃=10

Which I then put in a matrix and was able to reduce for the following solutions;

I₁=35/13
I₂=20/13
I₃=15/13

The problem is that the book states that I should be getting;

I₁=5/7
I₂=20/7
I₃=15/7

Where am I going wrong in setting up my equations? I know I'm not messing up going to RREF form cause my calculator is giving me the same answer. I figure I must be screwing up the initial equations.

 

[I like Serena]

Hi PullandTwist,

I believe your equations and solution are fine.
The stated book solution is wrong.
It looks as if it belongs to a similar problem with different resistors.
For instance with resistors $2\ \Omega, 2\ \Omega, 6\ \Omega$ and voltage $10\ \textrm{V}$.