Linear Dependence in \mathbb{R}^4?

[bwpbruce]

Question:
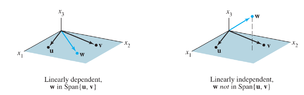
If [math]\textbf{v}_1,...,\textbf{v}_4[/math] are in [math]\mathbb{R}^4[/math] and [math]\{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3\}[/math] is linearly dependent, is [math]\{\textbf{v}_1, \textbf{v}_2, \textbf{v}_3, \textbf{v}_4\}[/math] also linearly dependent?

My Solution:
http://s29.postimg.org/4wvwjlkqd/Linearly_Independent_Sets.png

 

[Jameson]

No, it's only linearly independent if $c_1 = c_2 = c_3 = c_4 = 0$. I don't know if your intent is to help or to confuse further. If your linear algebra isn't up to par, then you shouldn't make contributions such as these.

That's a little rude. Since I own this site, I think I'll make contributions when I wish. My comment was not to confuse.

My comment was aiming towards this. If $\textbf{v}_4 \notin \text{Span}( \textbf{v}_1, \textbf{v}_2,\textbf{v}_3)$ then by definition $c_1 \textbf{v}_1+c_2 \textbf{v}_2+ c_3 \textbf{v}_3+ \ne c_4 \textbf{v}_4$, thus $c_1 \textbf{v}_1+c_2 \textbf{v}_2+ c_3 \textbf{v}_3- c_4\textbf{v}_4 \ne 0$ and they are in fact linearly independent but this isn't correct now that I think about it because $c_4$ can just be 0.

If you state that $c_4=0$ then your logic makes sense. The proof doesn't require two cases then and can be done as follows:

Assume $c_1 \textbf{v}_1+c_2 \textbf{v}_2+ c_3 \textbf{v}_3=0$ for some combination, not all 0, of $c_i$ by definition of linear dependence.

Then $c_1 \textbf{v}_1+c_2 \textbf{v}_2+ c_3 \textbf{v}_3+ 0\textbf{v}_4 = 0$ thus $(\textbf{v}_1, \textbf{v}_2, \textbf{v}_3, \textbf{v}_4)$ is linearly dependent.

 

[Nono713]

Your proof is perfectly fine to me, if a little opaque and long-winded. Intuitively, if $(v_1, v_2, v_3)$ are linearly dependent then adding any number of additional vectors doesn't change that: you can still express $v_1$ as a linear combination of $v_2, v_3$ and all the extra vectors. The fact that some coefficients are zero is immaterial, as long as at least one is nonzero, which is guaranteed by the assumption that $(v_1, v_2, v_3)$ are linearly dependent to begin with.

Another way to think of it is that every subset of a linearly independent set of vectors is linearly independent (the proof is exactly the same as above, simply add zero coefficients to show linear independence is preserved). Ergo, if you have a linearly dependent subset then your set can't be linearly independent. I hope that clears it up.

 

[bwpbruce]

How do you explain this then:
View attachment 3787
{$\textbf{u,v}$} is linearly dependent, yet they seem to be saying that {$\textbf{u,v,w}$} will be linearly independent if $\textbf{w}$ is not in span$\{\textbf{u,v}\}$

 

[Nono713]

How do you explain this then:
View attachment 3787
{$\textbf{u,v}$} is linearly dependent, yet they seem to be saying that {$\textbf{u,v,w}$} will be linearly independent if $\textbf{w}$ is not in span$\{\textbf{u,v}\}$

The set $(u, v)$ doesn't look linearly dependent to me in this picture. If they were linearly dependent then there would be a nontrivial solution to $t_1 u + t_2 v = 0$, that is, $u = cv$ for some nonzero scalar $c$. Here $u$ and $v$ are very clearly not coplanar since they span a plane of dimension 2 (and hence form a basis of that plane since they span it, and that basis is necessarily linearly independent).

 

[bwpbruce]

Explain again how $\textbf{u,v}$ are not co-planar again? I didn't understand it the first time you explained. They appear to be co-planar to me. You only need two dimensions to create a plane BTW.

 

[Nono713]

Explain again how $\textbf{u,v}$ are not co-planar again? I didn't understand it the first time you explained. They appear to be co-planar to me. You only need two dimensions to create a plane BTW.

Sorry, that was my mistake. I meant colinear, as per the linear dependence condition $u = cv$. What I mean is that they are not linearly dependent because one cannot be expressed as a linear combination of the other. Can you express $u$ as a (nontrivial) linear combination of $v$ (or vice versa)? If not, then they are linearly independent. (you can't, but you should try anyway)

 

[bwpbruce]

You at least helped me figure out what it was I was mis-understanding about this. I thank you for that.