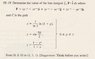sriracha
- 28
- 0
Problem statement attached. The correct way to do this seems to plug in your given x, y, z into F then integrate the dot product of F and <x',y',z'> dp from 0 to 1, however, this results in way too messy of an integral. Answer is 3/e.
<e^-(sin(pi*p/2))-((1-e^p)/(1-e))e^-(ln(1+p)/ln(2)),e^-((1-e^p)/(1-e))-(ln(1+p)/ln(2))e^-(sin(pi*p/2)),e^-(ln(1+p)/ln(2))-(sin(pi*p/2))e^-((1-e^p)/(1-e))>.<2^(x-1)ln(2),2/(pi*sqrt(1-y^2),(e-1)/((e-1)y+1)>
<e^-(sin(pi*p/2))-((1-e^p)/(1-e))e^-(ln(1+p)/ln(2)),e^-((1-e^p)/(1-e))-(ln(1+p)/ln(2))e^-(sin(pi*p/2)),e^-(ln(1+p)/ln(2))-(sin(pi*p/2))e^-((1-e^p)/(1-e))>.<2^(x-1)ln(2),2/(pi*sqrt(1-y^2),(e-1)/((e-1)y+1)>