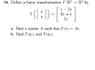Clandry
- 74
- 0
I attached the problem. I'm not sure if I'm misinterpreting the question, but this problem seems really easy, which is usually not the case with my class.
for part a) isn't that just the coefficient matrix of the right hand side?
This makes A:
1 -2
3 1
0 2
for part b) T(e1)=T[1 0]^t=[1 3 0]^t
T(e2)=T[0 1]^t=(-2 1 2)^t
Is this right?
for part a) isn't that just the coefficient matrix of the right hand side?
This makes A:
1 -2
3 1
0 2
for part b) T(e1)=T[1 0]^t=[1 3 0]^t
T(e2)=T[0 1]^t=(-2 1 2)^t
Is this right?