Linearity of differential equation

bhanesh
Messages
9
Reaction score
0
Friends I have one doubt

Below given equation is linear or non linear

1387027772743.jpg


:)
 
Physics news on Phys.org
It's non-linear, because of the cos x coefficient. Compare it to the ODE for a pendulum, which is non-linear, but can be linearized if small deflections are assumed.
 
bhanesh said:
Friends I have one doubt

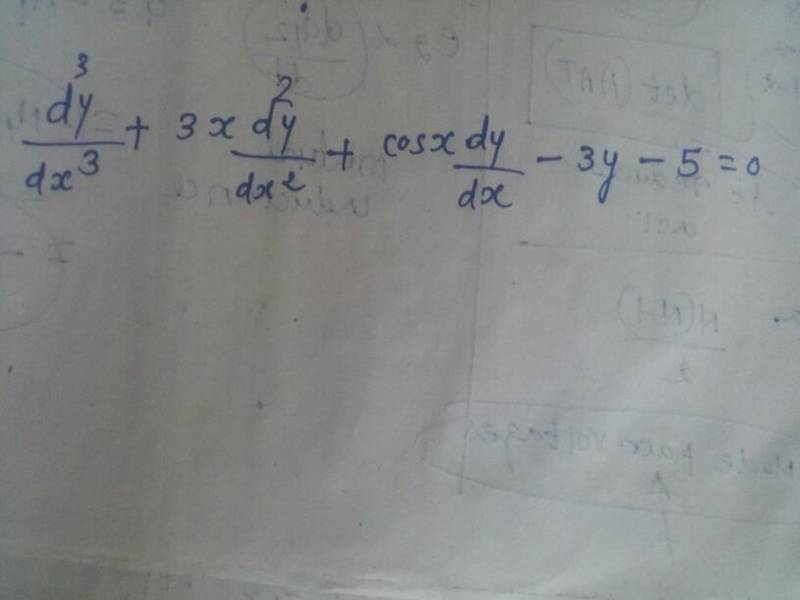
Below given equation is linear or non linear

View attachment 64770

:)
Mathematically,the equation you wrote is considered a linear ordinary differential equation with non-constant coefficients. It is considered linear if the homogeneous part is linear with respect to the dependent variable (in this case y).
 
But what about -5 term
 
bhanesh said:
But what about -5 term
That's not included in the homogeneous part.
 
Linear, because all exponents of y aren't different of +1.
 

Similar threads

I Explanation of all "its linearly independent derivatives"
Replies
3
Views
2K
I What are the applications of function-valued matrices?
Replies
5
Views
2K
I Number of solutions to the order of the equation
Replies
2
Views
2K
I Proving a basis is a basis for homogeneous linear differential equation with constant (complex) coefficients
Replies
2
Views
2K
I Why is this differential equation non-linear?
Replies
12
Views
2K
I When is an ODE (numerically) reversible in time?
Replies
4
Views
2K
I Second order non-homogeneous linear ordinary differential equation
Replies
2
Views
3K
A Is a solution of a differential equation a function of its parameters?
Replies
3
Views
1K
I Understanding Linearity of Differential Equations
Replies
8
Views
2K
I Maxwell's equations PDE interdependence and solutions
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top