Liquid flowing through a capacitor

[utkarshakash]

Homework Statement

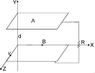
A parallel plate capacitor having plate area equal to A and the separation between the plates equal to d, is placed in a stream of conducting liquid with resistivity r. The liquid moves with constant velocity v parallel to the plates of capacitor. The complete system is placed in a uniform magnetic field of induction B, which is parallel to the plates of capacitor and perpendicular to direction of motion of liquid. The plates of capacitor are joined by some external resistance R. Calculate the amount of power generated in that resistance. What is the highest power equal to?

The Attempt at a Solution

Since power is being generated, current must be flowing in the circuit. But I don't have any idea what is the source of current here? I know this is somehow related to the flowing liquid but just can't figure out what's going on here. Any hints?

 

[NascentOxygen]

Magneto-hydrodynamics. The more common example is where the electrodes deliver current into salt water, and in the presence of a strong magnetic field, repulsion causes the water to be pumped away as a jet of water. You need a lot of current, and a strong magnetic field.

Your problem is just a modification of that.

 

[utkarshakash]

Magneto-hydrodynamics. The more common example is where the electrodes deliver current into salt water, and in the presence of a strong magnetic field, repulsion causes the water to be pumped away as a jet of water. You need a lot of current, and a strong magnetic field.

Your problem is just a modification of that.

"Magneto-hydrodynamics". never heard of this thing. can you give me some references on this topic?

 

[Yellowflash]

http://en.wikipedia.org.prx.websiteproxy.co.uk/wiki/Magnetohydrodynamics

 

[rude man]

Use the emf = Blv law on the section of volume under the plates covered by the liquid. Hint: the emf is constant but the resistance of the emf source starts at infinity and min's out when the liquid has completely filled the volume under the plates.

For calculating the max. power, no further information is needed, but if you wanted to derive P(t) you would need either the x or the y dimension of the plates. Or so I believe.